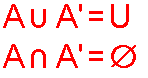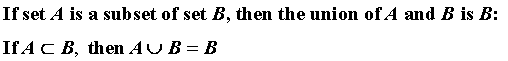Introduction to Sets
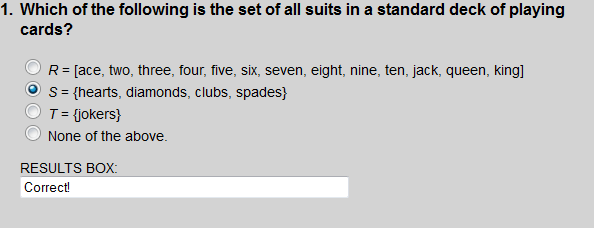
There are four suits in a standard deck of playing cards: hearts, diamonds, clubs and spades.
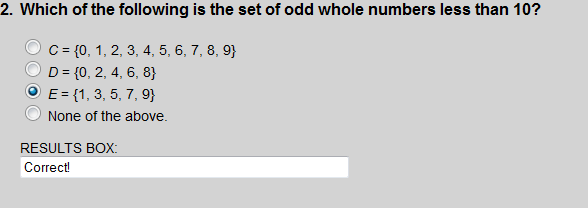
C is the set of whole numbers less than 10 and greater than or equal to 0. Set D is the even whole numbers less than 10, and set E is the odd whole numbers less than 10.
Set G is the set of all oceans on earth. Set E is a set of some rivers, and set F is a list of continents.
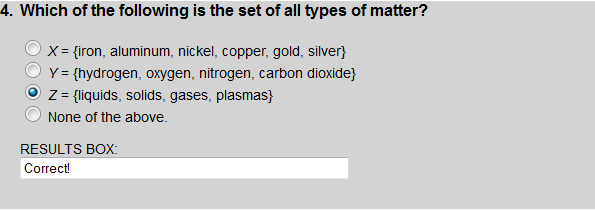
Set Z is the set of all types of matter. Set X is a set of some metals and set Y is a set of some gases.
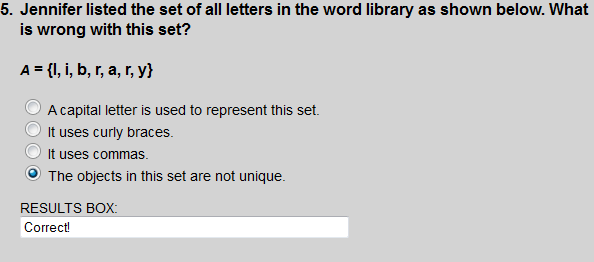
Set A lists the element r twice. So the objects in this set are not unique.
Basic Notation
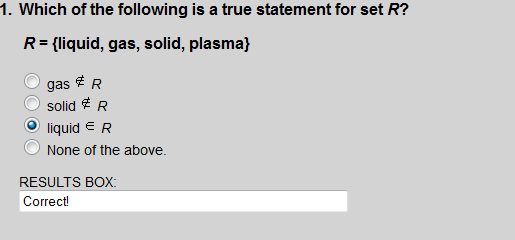
Liquid is an element of set R.
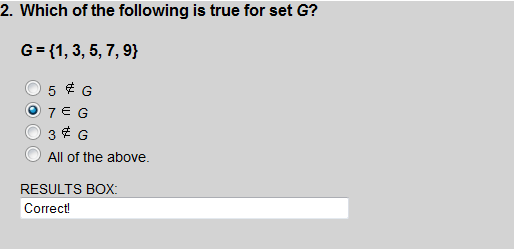
The number 7 is an element of set G.
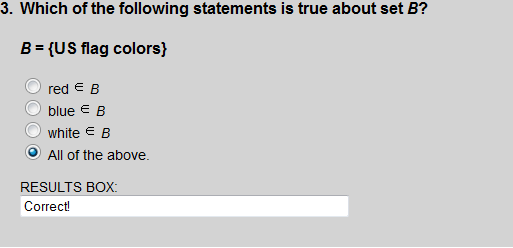
The colors red, white and blue are all colors of the US flag, and are all elements of set B.
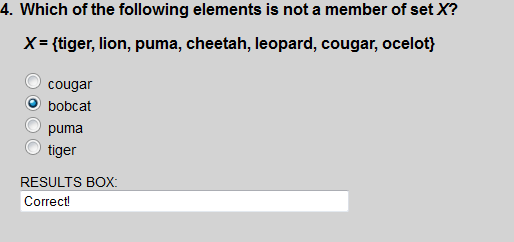
A bobcat was not listed in set X.
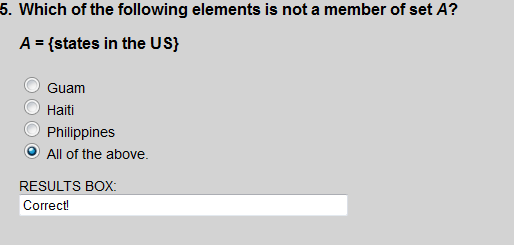
All of these territories are outside of the United States.
Types of Sets
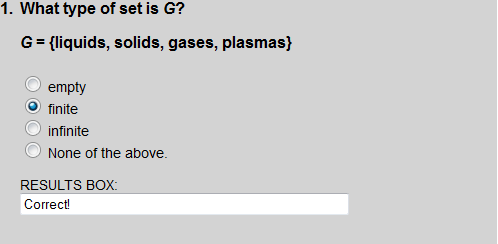
Set G has a finite number of elements.
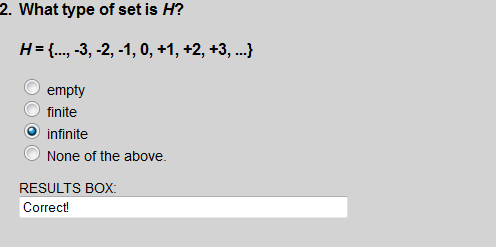
Set H is the set of integers, which has an infinite number of elements.
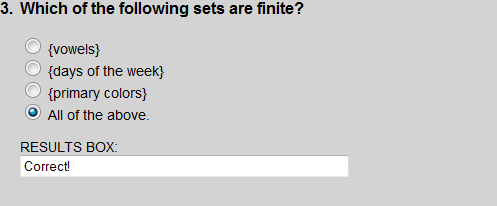
Each set listed in Exercise 3 is a finite set.
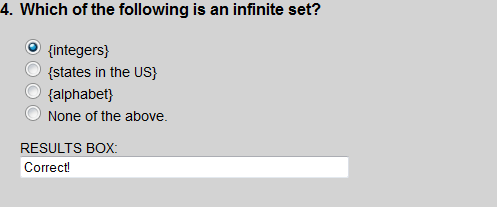
The integers is the only set in Exercise 4 that is infinite.
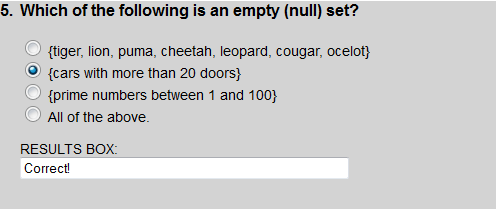
There are no cars with 20 doors, so this set is empty (null).
Set Equality
Since P and Y contain exactly the same number of elements, and the elements in both are the same, we say that P = Y.
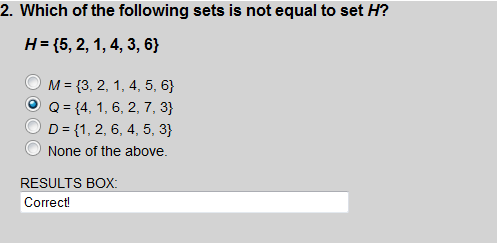
Set Q contains the element 7, which is not an element of set H. Thus H ≠Q
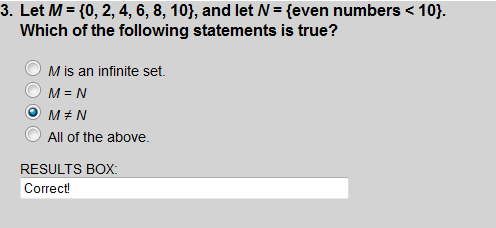
M = {0, 2, 4, 6, 8, 10} and N = {0, 2, 4, 6, 8}. Therefore M ≠N.
Since X and Y contain exactly the same number of elements, and the elements in both are the same, we say that X = Y.
Since A and B are both empty sets, we say that A = B.
Venn Diagrams
A = {2, 4, 6, 8} and the range given for A is non-inclusive.
Choice 1 uses the wrong notation, choice 2 is correct, choice 3 is wrong, and choice 4 is wrong.
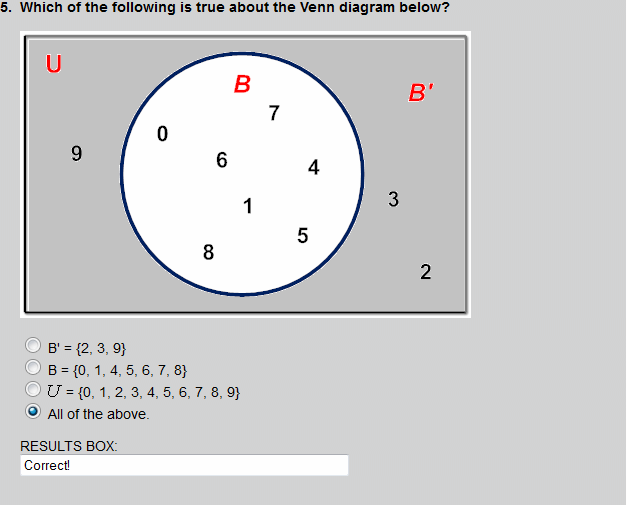
This Venn diagram represents the intersection of P and Q, which is 6.
The elements 2, 3, 5, 7, and 11 are all elements of X.
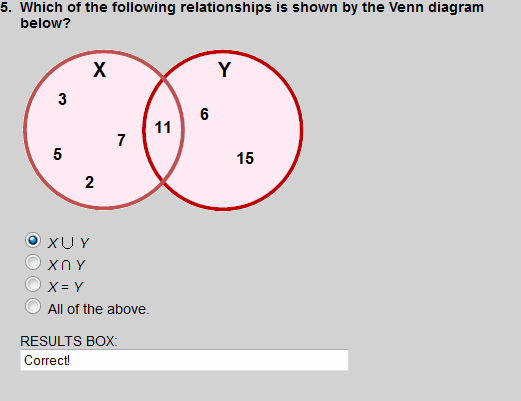
The union of X and Y is shown in this Venn diagram, by the shaded region.
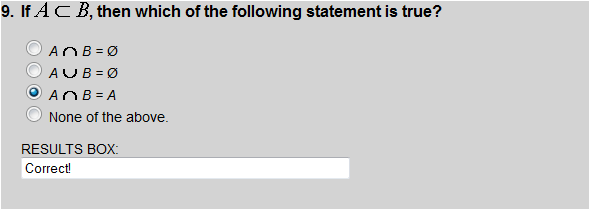
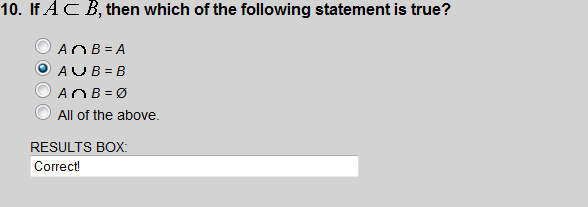
Subsets
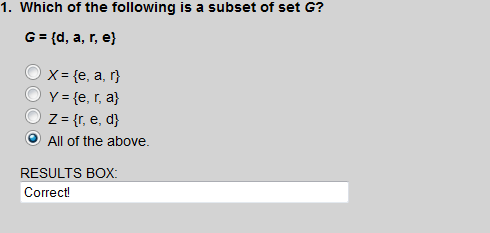
Sets X, Y, and Z are each subsets of set G.
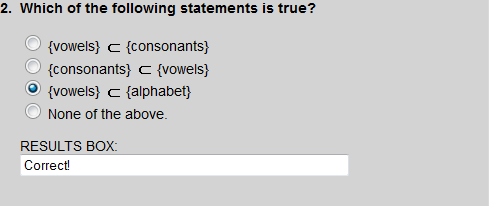
Every element of the set of vowels is contained in the set of the alphabet.
Since 9 is not an element of A, we know that C is not a subset of A.
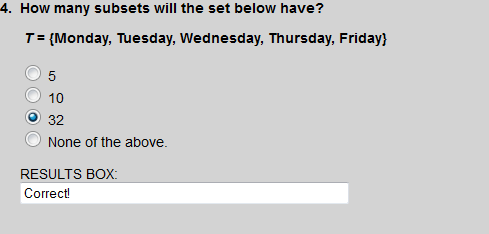
There are 5 elements in set T, so the number of subsets of T is 25, which equals 32.
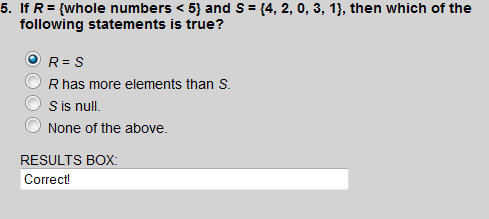
Set R = {0, 1, 2, 3, 4} and set S = {4, 3, 0, 2, 1}, thus R is equivalent to S.
Universal Set
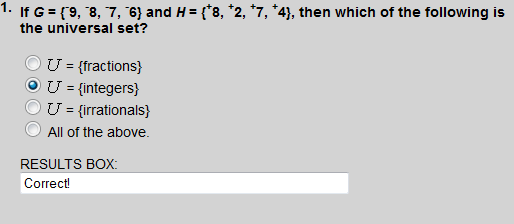
Each of the elements in set G and set H are integers. None of these elements are fractions nor irrationals.
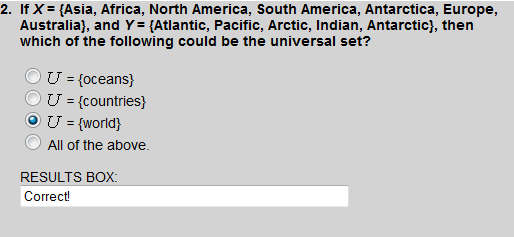
By definition, sets X and Y are each subsets of the universal set. So the world must be the universal set.
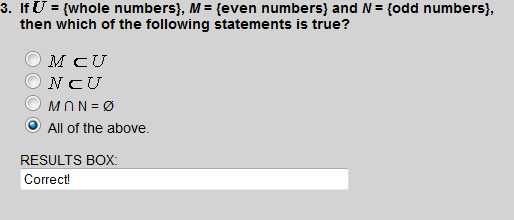
By definition, sets M and N are each subsets of the universal set. The intersection of M and N is null. So all of the above is the correct answer.
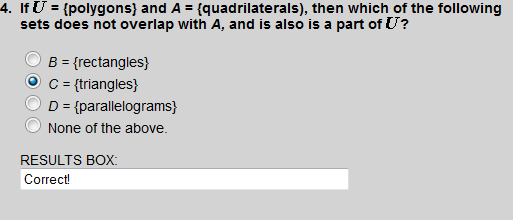
Triangles does not overlap with quadrilaterals, but triangles is a subset of the universal set (polygons).
Factors of 36 overlaps with set P, and is a subset of the set of whole numbers less than 40 (the universal set).
Set-Builder Notation
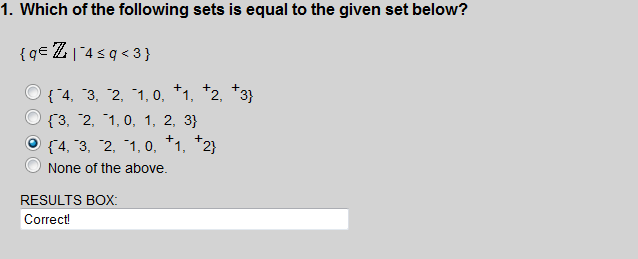
The set of all q such that q is an integer greater than or equal to -4 and less than 3.
The set of all x such that x is a real number greater than or equal to 4.
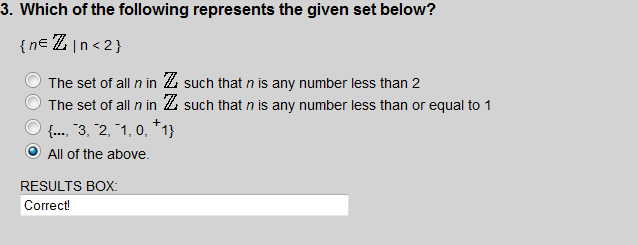
Each set listed is equal to "the set of all n such that n is an integer less than 2".
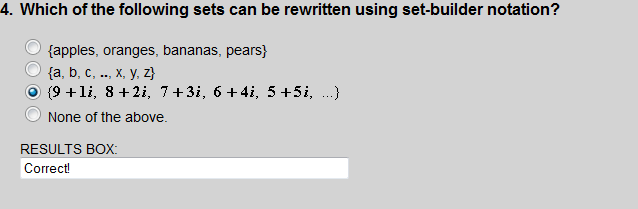
Set builder notation is usually used with infinite sets. Choices 1 and 2 are each finite sets that do not have numbers as their elements. By process of elimination, choice 3 makes sense.
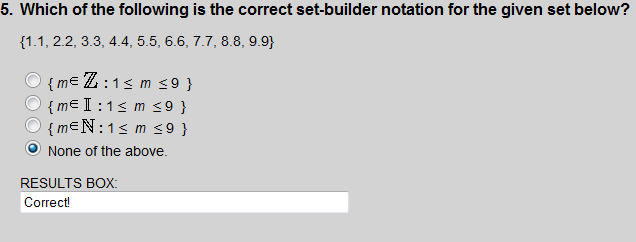
The elements given are real numbers. None of the choices (1-3) are sets with real-number elements.
Complement of a Set
The complement of a set is the set of elements which belong to 
but which do not belong to A.
X' = { n | n 
and n 
X }
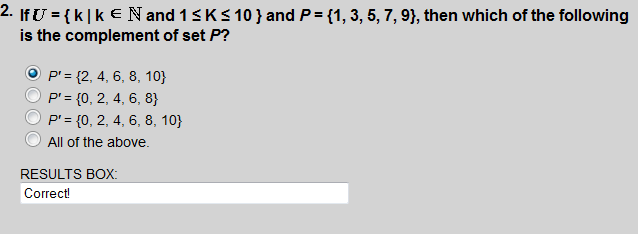
The complement of set P is the set of elements which belong to 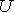but which do not belong to P.
The complement of set N is the set of elements which belong to (the alphabet) but which do not belong to N.
Draw a Venn diagram to help you find the answer.
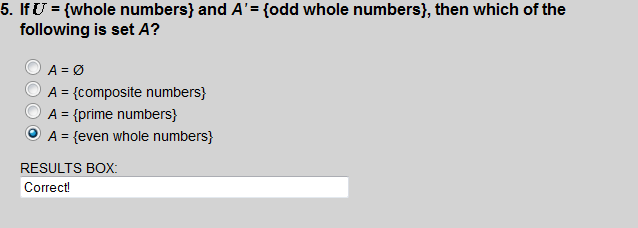
The complement of set A is the set of elements which belong to 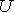but which do not belong to A.
A' = { x | x and x A }
Intersection
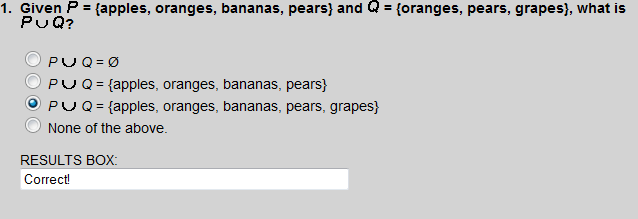
Oranges and pears are common to both sets.
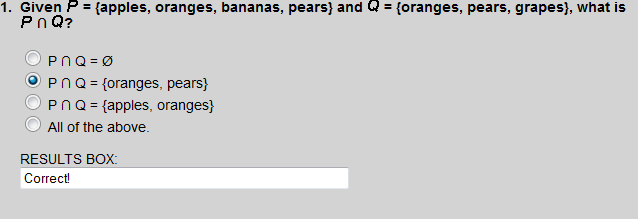
The number 2 is the only even prime.
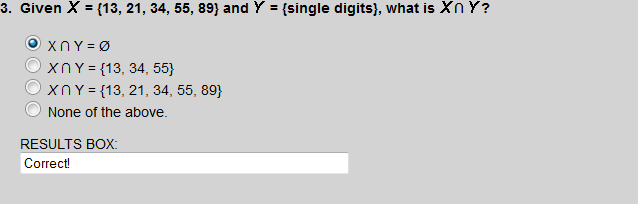
These sets have no elements in common.
The number 3 is an element of P, and is not in the intersection of P and Q.
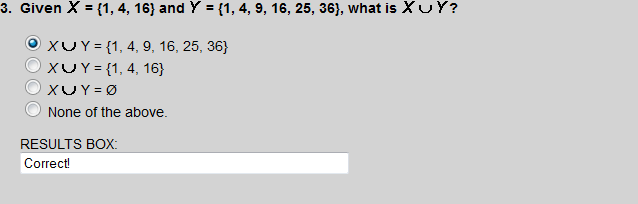
Union
A 
B = {x | x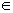
A or x
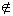B}
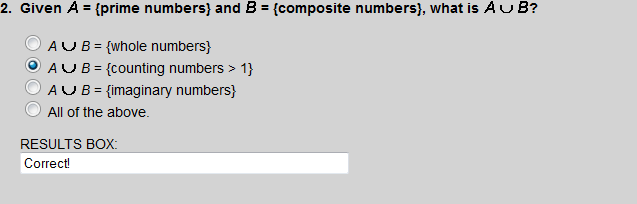
The numbers 0 and 1 are neither prime nor composite.
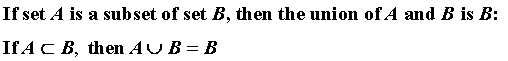
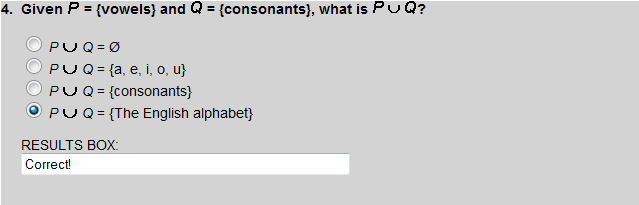
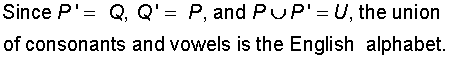
The union of a set and its complement is the Universal Set.
Practice Exercises
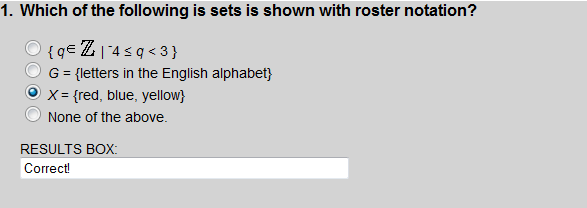
Choice 1 uses set-builder notation, choice 2 describes the set, and choice 3 uses roster notation.
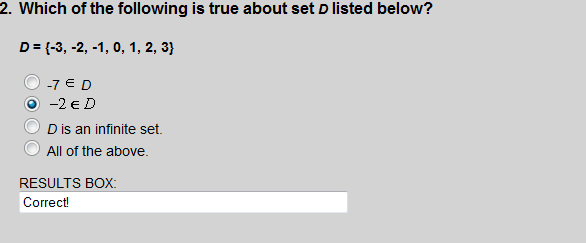
The element -2 is not an element of set D.
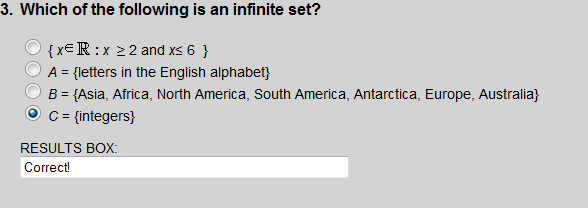
All of the sets listed are finite except choice 4.
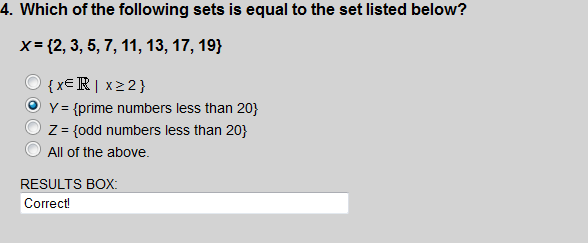
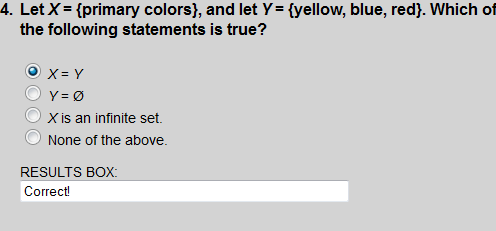
X = Y since X and Y contain exactly the same number of elements, and the elements in both are the same.
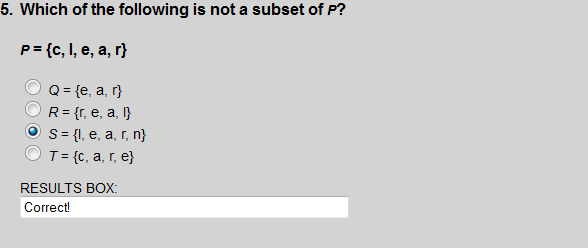
The element n is not a member of set P. So set S cannot be a subset of set P.
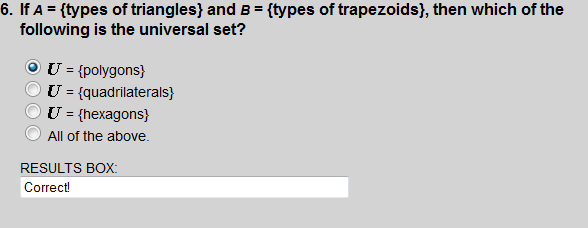
Both triangles ate trapezoids are subsets of polygons.
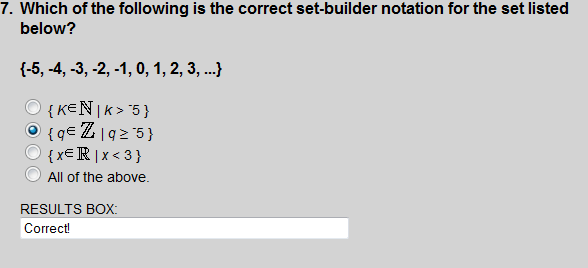
Choice 2 is the set of q such that q is an element of the integers, and q is greater than or equal to -5.
A' = { x | x and x A }
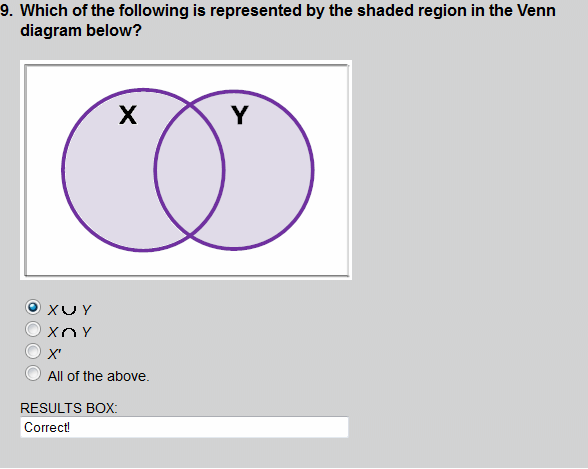
The shaded region shows a union of sets X and Y.
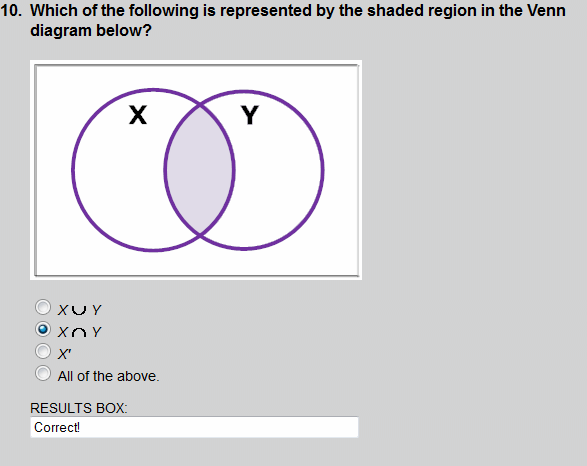
The shaded region shows an intersection of sets X and Y.
Challenge Exercises
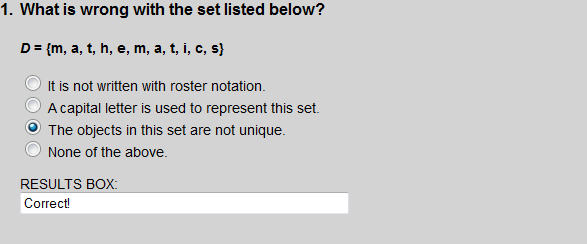
The letters m, a and t are listed more than once, so the objects are not unique.
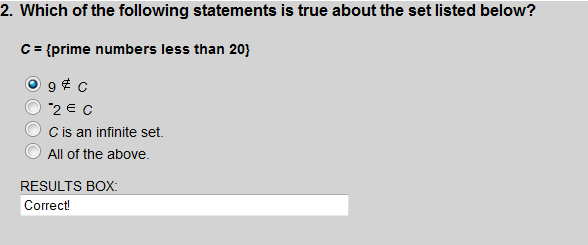
9 is not an element of C.
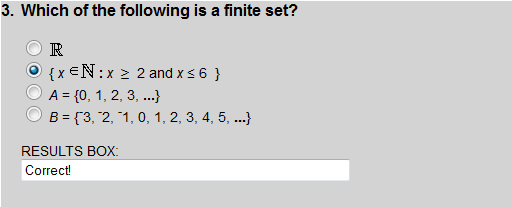
Choice 2 is a finite set; the rest are infinite.
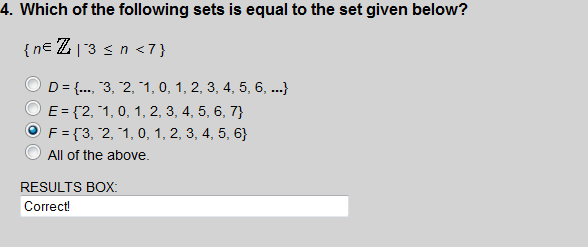
Choice 3 is equal to the set of n such that n is an element of the integers, and n is greater than or equal to -3 and less than 7.
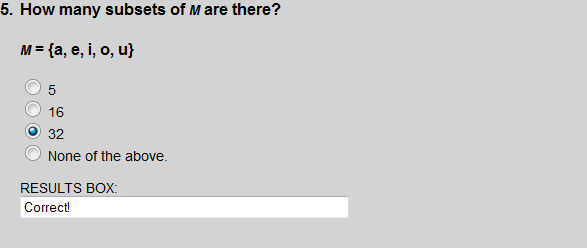
There are 5 elements in M, so the number of subsets is 25 which equal 32.
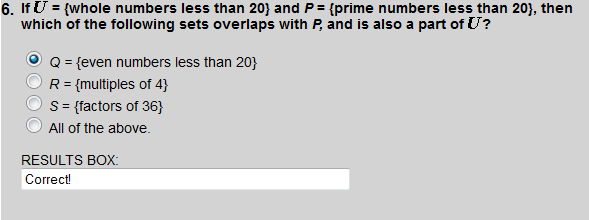
P = {2, 3, 5, 7, 11, 13, 17, 19} and Q = {2, 4, 6, 8, 10, 12, 14, 16, 18}. The element 2 is in the intersection of both sets.
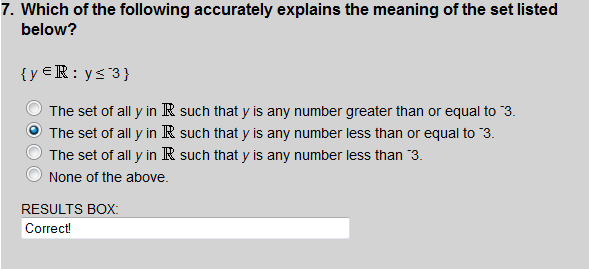
Choice 2 correctly describes the set given in set-builder notation.
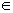
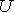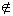Complement of a set is defined as: A' = { x | x and x A }
