In previous lessons, we learned that a set is a group of objects, and that Venn diagrams can be used to illustrate both set relationships and logical relationships.
Example 1: Given 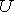 = {students who attend The Kewl School} and A = {students in Mrs. Glosser's class}. What is the set of all students who attend The Kewl School that are not in Mrs. Glosser's class?
= {students who attend The Kewl School} and A = {students in Mrs. Glosser's class}. What is the set of all students who attend The Kewl School that are not in Mrs. Glosser's class?
Analysis: The relationship between these sets is illustrated in the Venn diagram below.

Answer: The shaded area outside A represents all students who attend The Kewl School that are not in Mrs. Glosser's class.
In example 1, the shaded area represents the complement of Set A. The complement of A, denoted by A', consists of all students in The Kewl school that are not in Mrs. Glosser's class. Recall that a Universal Set is the set of all elements under consideration, denoted by capital 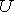 , and that all other sets are subsets of the Universal Set. Now we can define the complement of a set.
, and that all other sets are subsets of the Universal Set. Now we can define the complement of a set.
Definition: The complement of a set A, denoted by A', is the set of elements which belong to 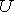 but which do not belong to A.
but which do not belong to A.
The complement of set A is denoted by A', You can also say "complement of A in 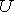 ", or "A-prime". We can now label the sets in example 1 using this notation.
", or "A-prime". We can now label the sets in example 1 using this notation.
Example 1: Given 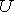 = {students who attend The Kewl School} and A = {students in Mrs. Glosser's class}. What is the set of all students who attend The Kewl School that are not in Mrs. Glosser's class?
= {students who attend The Kewl School} and A = {students in Mrs. Glosser's class}. What is the set of all students who attend The Kewl School that are not in Mrs. Glosser's class?
Analysis: The relationship between these sets is illustrated in the Venn diagram below.
Answer: The shaded area outside A represents A', which is all students who attend The Kewl School that are not in Mrs. Glosser's class.
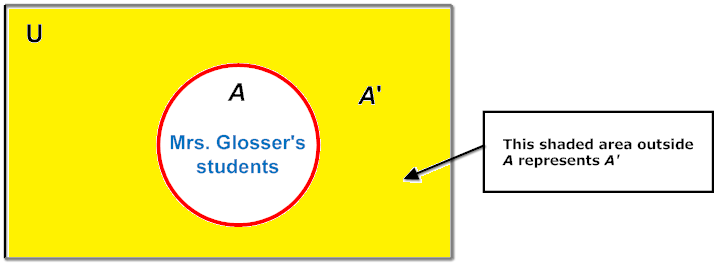
Another way to think of the complement of a set is as follow: Given set A, the complement of A is the set of all elements in the universal set  , that are not in A. Using set-builder notation, we can write:
, that are not in A. Using set-builder notation, we can write:
A' = { x | x 
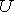 and x
and x 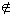 A }
A }
Let's find the complement of a set of numbers.
Example 2: Given 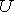 = {single digits} and B = {0, 1, 4, 5, 6, 7, 8}, find the complement of B.
= {single digits} and B = {0, 1, 4, 5, 6, 7, 8}, find the complement of B.
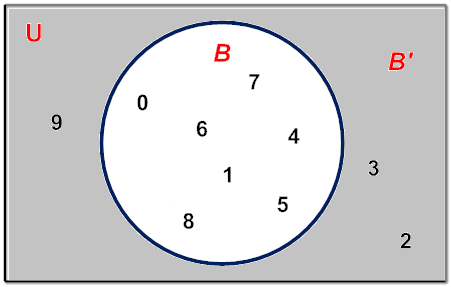
Answer: B' = {2, 3, 9}
Thus B' is the set of all numbers in 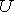 that are not in B. Using set-builder notation, we can write: B' = { x | x
that are not in B. Using set-builder notation, we can write: B' = { x | x 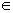
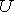 and x
and x 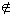 B }
B }
In examples 3 through 5, the universal set is the English alphabet.
Example 3: Given 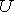 = {a, b, c, ..., x, y, z} and X = {a, b, c, d, e}, find X'.
= {a, b, c, ..., x, y, z} and X = {a, b, c, d, e}, find X'.
Analysis: X' would consist of all letters in the English alphabet that are not in X. This is shown in the Venn Diagram below.
Answer: X' = {f, g, h, ..., x, y, z}
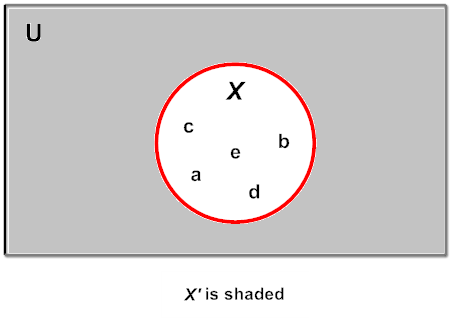
Example 4: Given  = {a, b, c, ..., x, y, z}, X = {a, b, c, d, e} and Y = {e, f, g}, find Y'.
= {a, b, c, ..., x, y, z}, X = {a, b, c, d, e} and Y = {e, f, g}, find Y'.
Analysis: Y' would consist of all letters in the English alphabet that are not in Y. This is shown in the Venn Diagram below..
Answer: Y' = {a, b, c, d, h, i, j, ..., x, y, z}
Example 5: Given 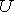 = {a, b, c, ..., x, y, z}, P = {a, b, c, d, e} and Q = {x, y, z}, find Q'.
= {a, b, c, ..., x, y, z}, P = {a, b, c, d, e} and Q = {x, y, z}, find Q'.
Analysis: Q' consists of all the letters in the alphabet that are not in Q. This is shown in the Venn Diagram below..
Answer: Q' = {a, b, c, d, e, f, g, h ..., u, v, w}
Looking at the examples above, a set and its complement have no elements in common. The union of a set and its complement is the Universal Set. The intersection of a set and its complement is the null set. These statements are summarized below:
Tips:
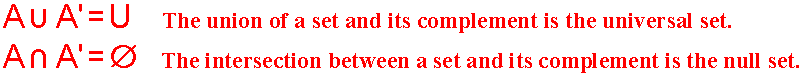
Notation Alert
There are several different ways to represent the complement of a set, as shown below.

All of these notations have the same meaning. However, for the purpose of this instructional unit, we have chosen to use A', read as A-prime.
Let's look at some examples of complement that involve set-builder notation and infinite sets.
Example 6: If 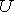 = { n | n
= { n | n 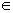
 and -6 < n < 7 } and B = { y | y even number; -5 < y < 6 }, then what is the complement of B?
and -6 < n < 7 } and B = { y | y even number; -5 < y < 6 }, then what is the complement of B?
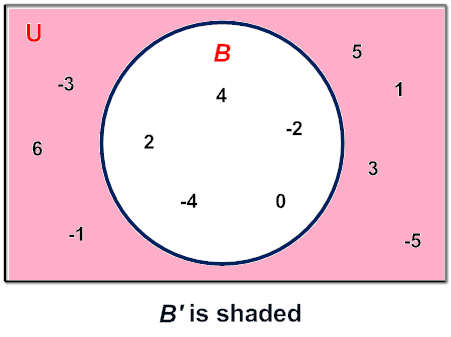
Answer: B' = {-5, -3, -1, 1, 3, 5, 6}
Example 7: Given 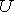 = {counting numbers > 1} and C = {prime numbers}, find C'.
= {counting numbers > 1} and C = {prime numbers}, find C'.
Analysis: C' would consist of all counting numbers greater than 1 that are not prime. This is shown in the Venn Diagram below.
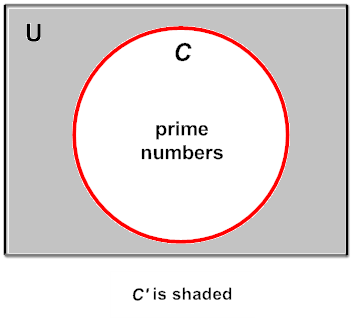
Answer: C' = {composite numbers}
Summary: Given set A, the complement of A is the set of all element in the universal set 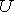 , that are not in A. The complement of set A is denoted as A' and is read as A-prime. The formal definition of complement is shown below.
, that are not in A. The complement of set A is denoted as A' and is read as A-prime. The formal definition of complement is shown below.
A' = { x | x 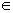
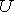 and x
and x 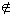 A }
A }
Exercises
Directions: Read each question below. You may draw a Venn diagram to help you find the answer to each exercise. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, rethink your answer, then choose a different button.
| 1. | If 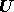 = {students who attend a school} and X' = {students who do not ride the bus}, then which of the following is setX? = {students who attend a school} and X' = {students who do not ride the bus}, then which of the following is setX? |
| 2. | If 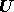 = { k | k = { k | k 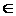 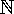 and 1 ≤ K ≤ 10 } and P = {1, 3, 5, 7, 9}, then which of the following is the complement of set P? and 1 ≤ K ≤ 10 } and P = {1, 3, 5, 7, 9}, then which of the following is the complement of set P? |
| 3. | Given 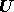 = {a, b, c, ..., x, y, z}, M = {a, b, c} and N = {c, d, e}, find N'. = {a, b, c, ..., x, y, z}, M = {a, b, c} and N = {c, d, e}, find N'. |
| 4. | If 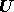 = { n | -7 < n < 8 } and P = {-6, -4, -2, 4, 6}, then which of the following is the complement of set P? = { n | -7 < n < 8 } and P = {-6, -4, -2, 4, 6}, then which of the following is the complement of set P? |
| 5. | If 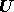 = {whole numbers} and A' = {odd whole numbers}, then which of the following is set A? = {whole numbers} and A' = {odd whole numbers}, then which of the following is set A? |




