In previous lessons, we used Venn diagrams to represent relationships between sets. Let's look at the relationship of the sets described in example 1 below.
Example 1: Let X = {1, 2, 3} and Let Y = {3, 4, 5}. What elements do X and Y have in common?
Analysis: We will draw a Venn diagram of two overlapping circles. Elements that are common to both sets will be placed in the middle part, where the circles overlap.
Solution:
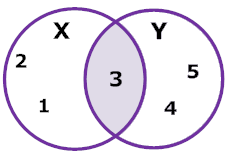
Explanation: The circle on the left represents set X and the circle on the right represents set Y. The shaded region in the middle is what they have in common. That is their intersection. The intersection of sets X and Y is 3.
The Venn Diagram in example 1 makes it easy to see that the number 3 is common to both sets. So the intersection of X and Y is 3, and this is written as:
X ∩ Y = {3}
| Definition: | The intersection of two sets, X and Y, is the set of elements that are common to both X and Y. It is denoted by X ∩ Y, and is read "X intersect Y". |
So the intersection of two sets is the set of elements common to both sets. Let's look at some more examples of intersection.
Example 2: Let 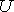 = {counting numbers}, P = {multiples of 3 less than 20} and Q = {even numbers less than 20}. Draw and label a Venn diagram to show the intersection of P and Q.
= {counting numbers}, P = {multiples of 3 less than 20} and Q = {even numbers less than 20}. Draw and label a Venn diagram to show the intersection of P and Q.
Analysis: Start by filling in the elements in the intersection. Since P = {3, 6, 9, 12, 15, 18} and Q = {2, 4, 6, 8, 10, 12, 14, 16, 18}, we know that 6, 12 and 18 will be filled in first.
Solution:
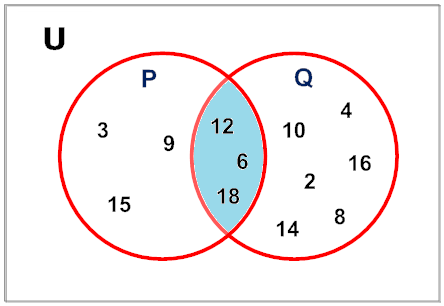
Notation: P ∩ Q = {6, 12, 18}
Another way to define the intersection of two sets is as follows:
A ∩ B = { x | x 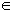 A and x
A and x 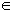 B }
B }
The procedure for drawing the intersection of two sets is shown below.
Procedure for Drawing the Intersection of Two Sets Overlapping Sets
Step 1:
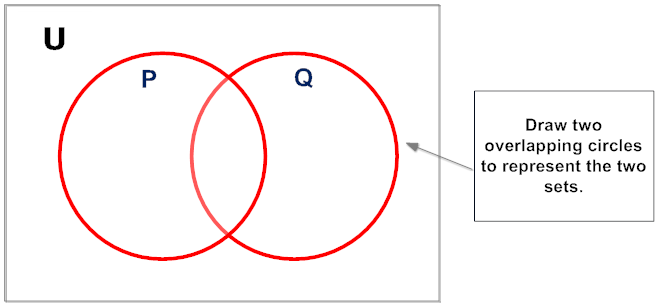
Step 2:
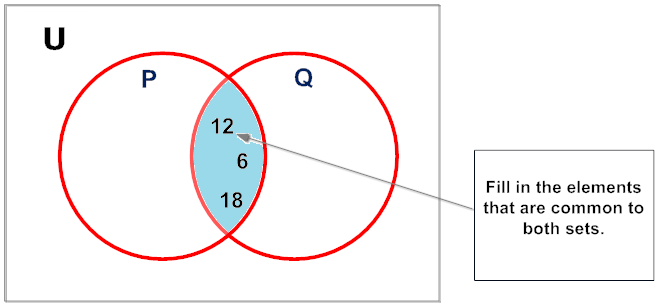
Step 3:
Let's look at the intersection of other types of sets. In example 3 below, the given sets are not overlapping.
Example 3: Let 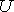 = {animals}, A = {dogs} and B = {cats}. Draw and label a Venn diagram to show the intersection of A and B.
= {animals}, A = {dogs} and B = {cats}. Draw and label a Venn diagram to show the intersection of A and B.
Analysis: Sets A and B do not overlap. These sets are disjoint, and have no elements in common.
Solution:
Notation: A ∩ B= Ø
Two sets A and B are disjoint if their intersection is null. This is denoted by A ∩ B = Ø, where Ø is the null or empty set.
Recall that a Universal Set is the set of all elements under consideration, denoted by capital  . All other sets are subsets of the universal set. So in each example above, the circles are subsets of the Universal set. We have examined the intersection of overlapping sets, and of disjoint sets. Let's look at the intersection of one set contained within another.
. All other sets are subsets of the universal set. So in each example above, the circles are subsets of the Universal set. We have examined the intersection of overlapping sets, and of disjoint sets. Let's look at the intersection of one set contained within another.
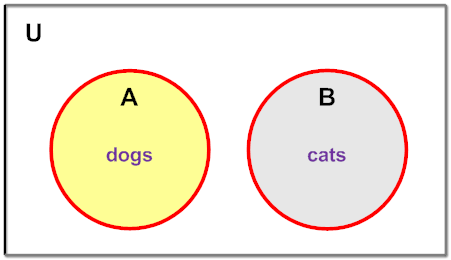
Example 4: Let C = {a, r, e} and D = {f, a, i, r, e, s, t}. Draw and label a Venn diagram to show the intersection of sets C and D.
Analysis: C is a subset of D. Recall that this is denoted by C D.
Solution:
Explanation: It turns out that C ∩ D = {a, r, e}, which is equal to the set C.
In example 4, since C 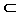 D , we get that C ∩ D = C. This relationship is defined below.
D , we get that C ∩ D = C. This relationship is defined below.

The procedure for drawing the intersection of one set contained within another is shown below.
| Procedure for Drawing the Intersection of One Set Contained Within Another | |
| Step 1: | Draw one circle within another circle. |
| Step 2: | Write down the elements in the inner circle. |
| Step 3: | Write down the remaining elements in the outer circle. |
Let's see if you can follow the challenge presented in Example 5.
Example 5: Given the Venn diagram below, name a member of Band that is not in both Band and Chorus.
Analysis: This problem is asking us to find a member of Band that is not in the intersection of Band and Chorus.
Solution:
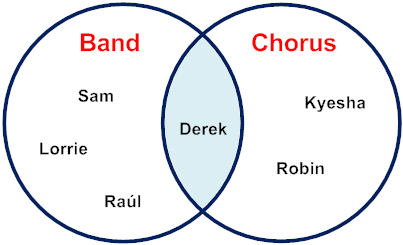
Explanation: Sam, Lorrie and Raúl are each members of Band only. In addition, these students are not in Band and Chorus.
Summary: The intersection of two sets A and B, denoted by A ∩ B, is the set of elements that are common to both A and B. The formal definition of intersection is shown below.
A ∩ B = { x | x 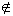 A and x
A and x 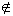 B}
B}
Exercises
Directions: Draw and label a Venn Diagram to help you answer each question below. Select your answer by clicking on the corresponding button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, rethink your answer, then choose a different button.
| 1. | Given 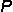 = {apples, oranges, bananas, pears} and = {apples, oranges, bananas, pears} and 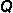 = {oranges, pears, grapes}, what is = {oranges, pears, grapes}, what is 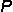 ∩ ∩ 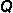 ? ? |
|
|
|
| 2. | Given 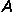 = {even whole numbers} and = {even whole numbers} and 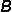 = {prime numbers}, what is = {prime numbers}, what is 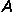 ∩ ∩ 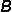 ? ? |
| 3. | Given 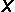 = {13, 21, 34, 55, 89} and = {13, 21, 34, 55, 89} and 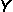 = {single digits}, what is = {single digits}, what is 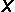 ∩ ∩ 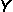 ? ? |
| 4. | Given 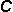 = {Saturday, Sunday} and = {Saturday, Sunday} and 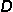 = {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}, what is = {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}, what is 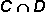 ? ? |
| 5. | Given the Venn diagram below, which of the following is an element of 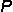 , and not an element of ( , and not an element of ( ∩ ∩  )? )? |
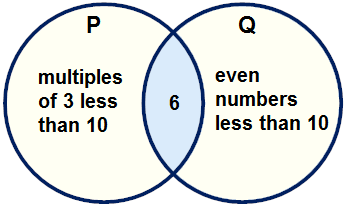 |
|




