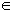Problem: Mrs. Glosser asked Kyesha, Angie and Eduardo to list the set all of integers greater than -3.
Problem: Mrs. Glosser asked Kyesha, Angie and Eduardo to list the set all of integers greater than -3.
Analysis: Each student wrote this set using different notation.
Solution:
| Kyesha | P = {-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...} |
| Angie | P = {-2, -1, 0, +1, +2, +3, +4, +5, +6, +7, +8, +9, +10, +11, ...} |
| Eduardo | P = {all integers greater than -3} |
Each of the students in the problem above used correct notation! However, Mrs. Glosser told them that there was another way to write this set:
P = {x : x is an integer, x > -3 }, which is read as: “P is the set of elements x such that x is an integer greater than -3.”
Mrs. Glosser used set-builder notation, a shorthand used to write sets, often sets with an infinite number of elements. Let's look at some more examples.
| Example | Set-Builder Notation | Read as | Meaning |
| 1 | {x : x > 0} | the set of all x such that x is greater than 0. | any value greater than 0 |
| 2 | {x : x ≠ 11} | the set of all x such that x is any number except 11. | any value except 11 |
| 3 | {x : x < 5} | the set of all x such that x is any number less than 5. | any value less than 5 |
Each of these sets is read aloud exactly the same way when the colon : is replaced by a vertical line | as in {x | x > 0}. Both the colon and the vertical line represent the words "such that". Let's look at these examples again.
| Example | Set-Builder Notation | Read as | Meaning | |
| with : | with | | |||
| 1 | {x : x > 0} | {x | x > 0} | the set of all x such that x is greater than 0 | any value greater than 0 |
| 2 | {x : x ≠ 11} | {x | x ≠ 11} | the set of all x such that x is any number except 11 | any value except 11 |
| 3 | {x : x < 5} | {x | x < 5} | the set of all x such that x is any number less than 5 | any value less than 5 |
Note that the "x" is just a place-holder, it could be anything, such as { q | q > 0 }.
The general form of set-builder notation is:
General Form: {formula for elements : restrictions} or {formula for elements | restrictions}
Types of Numbers
In the examples above, we examined values with set-builder notation. However, we did not specify what type of number these values can be. With set-builder notation, we normally show what type of number we are using. For example, look at x below:
{x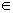
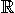 | x > 3 }
| x > 3 }
Recall that 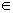 means "a member of", or simply "in".
means "a member of", or simply "in". 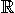 is the special symbol for Real Numbers. So x
is the special symbol for Real Numbers. So x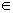
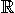 means "all x in
means "all x in 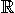 ".
".
Thus, {x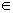
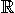 | x > 3 } means "the set of all x in
| x > 3 } means "the set of all x in 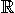 such that x is any number greater than 3." (In other words, x is all real numbers greater than 3.)
such that x is any number greater than 3." (In other words, x is all real numbers greater than 3.)
There are other types of numbers besides Real Numbers. Here are some common types used in mathematics.
| Common Types of Numbers | |||||
 |
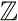 |
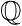 |
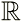 |
 |
 |
| Natural Numbers | Integers | Rational Numbers | Real Numbers | Imaginary Numbers | Complex Numbers |
Whole Numbers start at zero and go up by one forever (no fractions). The set of whole numbers is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
Counting Numbers are whole numbers greater than zero. (You cannot count with zero!) The set of counting numbers is {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
Natural Numbers are whole, non-negative numbers, denoted by 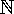 . This can mean either "Counting Numbers", with
. This can mean either "Counting Numbers", with 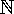 = {1, 2, 3, ...}, or "Whole Numbers", with
= {1, 2, 3, ...}, or "Whole Numbers", with 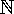 = {0, 1, 2, 3, ...}.
= {0, 1, 2, 3, ...}.
Integers are the set of whole numbers and their opposites. These numbers can be negative, positive, or zero. Integers are denoted by 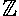 , with
, with 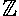 = {..., -3, -2, -1, 0, +1, +2, +3, ...}.
= {..., -3, -2, -1, 0, +1, +2, +3, ...}.
Real Numbers are denoted by the letter 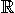 . Positive or negative, large or small, whole numbers or decimal numbers are all Real Numbers. A real number is any positive or negative number. This includes all integers and all rational and irrational numbers. Rational numbers, denoted by
. Positive or negative, large or small, whole numbers or decimal numbers are all Real Numbers. A real number is any positive or negative number. This includes all integers and all rational and irrational numbers. Rational numbers, denoted by 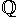 , may be expressed as a fraction (such as 7/8) and irrational numbers may be expressed by an infinite decimal representation (3.1415926535...). These numbers are called "Real Numbers" because they are not Imaginary Numbers.
, may be expressed as a fraction (such as 7/8) and irrational numbers may be expressed by an infinite decimal representation (3.1415926535...). These numbers are called "Real Numbers" because they are not Imaginary Numbers.
An Imaginary Number is a number which when squared, gives a negative result. There is such a number, called i, which when squared, equals negative 1. This is shown below:
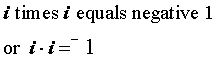
When we take the square root of i, we get this algebraic result:
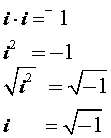
Thus, i is equal to the square root of negative 1. Imaginary numbers are defined as part of the Complex Numbers as shown below.
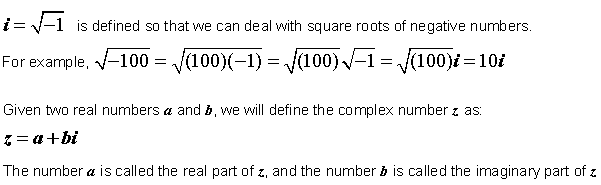
In short, a Complex Number is a number of the form a+bi where a and b are real numbers and i is the square root of -1.
The definitions of these numbers may be somewhat elaborate. However, the important thing to realize is that each type of number listed above is an infinite set, and that set-builder notation is often used to describe such sets. Let's look at some examples of set-builder notation.
| Example 4 | Read | Meaning |
{ K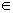 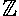 | k > 5 } | k > 5 } |
the set of all k in 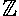 , such that k is any number greater than 5 , such that k is any number greater than 5 |
all integers greater than 5 |
Note that we could also write this set as {6, 7, 8, ...}. Therefore, we can say that { K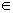
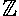 | k > 5 } = {6, 7, 8, ...}, and that these sets are equal. Set-Builder Notation is also useful when working with an interval of numbers, as shown in the examples below.
| k > 5 } = {6, 7, 8, ...}, and that these sets are equal. Set-Builder Notation is also useful when working with an interval of numbers, as shown in the examples below.
| Example | Set-Builder Notation | Read | Also Written As |
| 5 | { q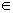 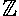 | 2 < q < 6 } | 2 < q < 6 } |
the set of all q in 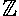 , such that q is any number between 2 and 6 , such that q is any number between 2 and 6 |
{3, 4, 5} |
| 6 | { p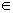 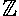 | 2 ≤ p ≤ 6 } | 2 ≤ p ≤ 6 } |
the set of all p in 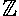 such that p is any number between 2 and 6, inclusive. such that p is any number between 2 and 6, inclusive. |
{2, 3, 4, 5, 6} |
| 7 | { n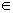 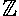 | 2 ≤ n < 6 } | 2 ≤ n < 6 } |
the set of all n in 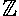 such that n is any number greater than or equal to 2 and less than 6. such that n is any number greater than or equal to 2 and less than 6. |
{2, 3, 4, 5} |
Why use set-builder notation?
You may be wondering about the need for such complex notation. If you have the set of all integers between 2 and 6, inclusive, you could simply use roster notation to write {2, 3, 4, 5, 6}, which is probably easier than using set-builder notation:
{ q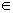
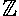 : 2 ≤ q ≤ 6 }
: 2 ≤ q ≤ 6 }
But how would you list the Real Numbers in the same interval? Using roster notation doesn't make much sense in this case:
{2, 2.1, 2.01, 2.001, 2.0001, ... ??? }
To express the set of real numbers above, it is better to use set-builder notation. Start with all Real Numbers, then limit them to the interval between 2 and 6, inclusive.
{ x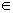
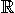 : x ≥ 2 and x ≤ 6 }
: x ≥ 2 and x ≤ 6 }
You can also use set builder notation to express other sets, such as this algebraic one:
{ x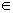
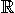 : x = x2 }
: x = x2 }
When you evaluate this equation algebraically, you get:
| Step | Evaluate | Explanation |
| 1 | x = x2 | Original equation |
| 2 | x2 - x = 0 | Subtract x from both sides |
| 3 | x(x-1) = 0 | Solve for x to find the roots of this equation |
| 4 | x =0 or x - 1 = 0 | If the product of two factors is zero, then each factor can be set equal to zero. |
| 5 | x - 1 = 0 | For the second factor, add 1 to both sides |
| 5 | x = 0 or x = 1 | Solution {0, 1} |
Thus { x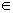
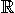 : x = x2 } = {0, 1}
: x = x2 } = {0, 1}
Summary: Set-builder notation is a shorthand used to write sets, often for sets with an infinite number of elements. It is used with common types of numbers, such as integers, real numbers, and natural numbers. This notation can also be used to express sets with an interval or an equation.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, rethink your answer, then choose a different button.
| 1. | Which of the following sets is equal to the given set below?
{ q |
| 2. | Which of the following accurately explains the meaning of the given set below?
{ x |
| 3. | Which of the following represents the given set below?
{ n |
| 4. | Which of the following sets can be rewritten using set-builder notation? |
| 5. | Which of the following is the correct set-builder notation for the given set below?
{1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9} |