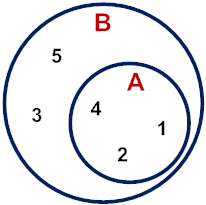
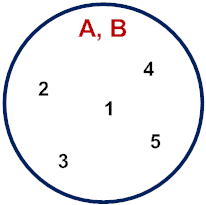
Example 1: Given A = {1, 2, 4} and B = {1, 2, 3, 4, 5}, what is the relationship between these sets?
We say that A is a subset of B, since every element of A is also in B. This is denoted by:
A Venn diagram for the relationship between these sets is shown to the right.
Answer: A is a subset of B.
Another way to define a subset is: A is a subset of B if every element of A is contained in B. Both definitions are demonstrated in the Venn diagram above.
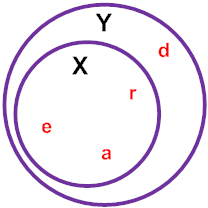Example 2: Given X = {a, r, e} and Y = {r, e, a, d}, what is the relationship between these sets?
We say that X is a subset of Y, since every element of X is also in Y. This is denoted by:
A Venn diagram for the relationship between these sets is shown to the right.
Answer: X is a subset of Y.
Example 3: Given P = {1, 3, 4} and Q = {2, 3, 4, 5, 6}, what is the relationship between these sets?
We say that P is not a subset of Q since not every element of P is not contained in Q. For example, we can see that 1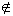 
Q. The statement "P is not a subset of Q" is denoted by:
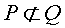
Note that these sets do have some elements in common. The intersection of these sets is shown in the Venn diagram below.
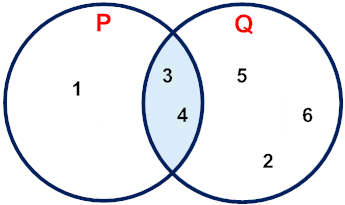
Answer: P is not a subset of Q.
The notation for subsets is shown below.
| Symbol | Meaning |
 |
is a subset of |
 |
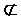is not a subset of |
Example 4: Given A = {1, 2, 3, 4, 5} and B = {3, 1, 2, 5, 4}, what is the relationship between A and B?
Analysis: Recall that the order in which the elements appear in a set is not important. Looking at the elements of these sets, it is clear that:
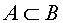
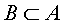
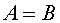
Answer: A and B are equivalent.
Definition: For any two sets, if A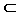 
B and B 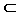A, then A = B. Thus A and B are equivalent.
Example 5: List all subsets of the set C = {1, 2, 3}.
Answer:
| Subset | List all possible combinations of elements... |
| D = {1} | one at a time |
| E = {2} | one at a time |
| F = {3} | one at a time |
| G = {1, 2} | two at a time |
| M = {1, 3} | two at a time |
| N = {2, 3} | two at a time |
| P = {1, 2, 3} | three at a time |
| Ø | The null set has no elements. |
Looking at example 5, you may be wondering why the null set is listed as a subset of C. There are no elements in a null set, so there can be no elements in the null set that aren't contained in the complete set. Therefore, the null set is a subset of every set. You may also be wondering: Is a set a subset of itself? The answer is yes: Any set contains itself as a subset. This is denoted by:
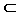A A.
A subset that is smaller than the complete set is referred to as a proper subset. So the set {1, 2} is a proper subset of the set {1, 2, 3} because the element 3 is not in the first set. In example 5, you can see that G is a proper subset of C, In fact, every subset listed in example 5 is a proper subset of C, except P. This is because P and C are equivalent sets (P = C). Some mathematicians use the symbol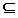 
to denote a subset and the symbol 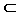to denote a proper subset, with the definition for proper subsets as follows:
If A 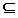B, and A ≠ B, then A is said to be a proper subset of B and it is denoted by A 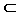B.
While it is important to point out the information above, it can get a bit confusing, So let's think of subsets and proper subsets this way:
| Subsets and Proper Subsets |
| The set {1, 2} is a proper subset of the set {1, 2, 3}. |
| The set {1, 2, 3} is a not a proper subset of the set {1, 2, 3}. |
Do you see a pattern in the examples below?
Example 6: List all subsets of the set R = {x, y, z}. How many are there?
| Subsets |
| D = {x} |
| E = {y} |
| F = {z} |
| G = {x, y} |
| H = {x, z} |
| J = {y, z} |
| K = {x, y, z} |
| Ø |
Answer: There are eight subsets of the set R = {x, y, z}.
Example 7: List all subsets of the set C = {1, 2, 3, 4}. How many are there?
| Subsets | |
| D = {1} | M = {2, 4} |
| E = {2} | N = {3, 4} |
| F = {3} | O = {1, 2, 3} |
| G = {4} | P = {1, 2, 4} |
| H = {1, 2} | Q = {1, 3, 4} |
| J = {1, 3} | R = {2, 3, 4} |
| K = {1, 4} | S = {1, 2, 3, 4} |
| L = {2, 3} | Ø |
Answer: There are 16 subsets of the set C = {1, 2, 3, 4}.
In example 6, set R has three (3) elements and eight (8) subsets. In example 7, set C has four (4) elements and 16 subsets. To find the number of subsets of a set with n elements, raise 2 to the nth power: That is:
The number of subsets in set A is 2n , where n is the number of elements in set A.
L e s s o n S u m m a r y
Subset: A is a subset of B: if every element of A is contained in B. This is denoted by A 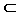B.
Equivalent Sets: For any two sets, if A 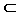B and B 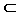A, then A = B.
Null set: The null set is a subset of every set.
Sets and subsets: Any set contains itself as a subset. This is denoted by 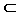A A.
Proper Subsets: If A 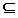B, and A ≠ B, then A is said to be a proper subset of B and it is denoted by A 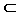B.
Number of Subsets: The number of subsets in set A is 2n , where n is the number of elements in set A.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, rethink your answer, then choose a different button.
| 1. | Which of the following is a subset of set G?
G = {d, a, r, e} |
| 2. | Which of the following statements is true? |
| 3. | Which of the following is NOT a subset of set A?
A = {2, 3, 5, 7, 11} |
| 4. | How many subsets will the set below have?
T = {Monday, Tuesday, Wednesday, Thursday, Friday} |
| 5. | If R = {whole numbers < 5} and S = {4, 2, 0, 3, 1}, then which of the following statements is true? |
