Example 1: Dana will pay for her new car in 48 monthly payments. If her car loan is for $24,561, then how much will Dana pay each month? Round your answer to nearest cent.
Analysis: We need to divide $24,561 into 48 equal amounts. To solve this problem, we will divide $24,561 by 48, and then round the quotient to the nearest hundredth.
Step 1: Divide. Write zeros to the right of the last digit in the dividend, if necessary.
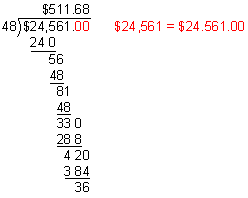
Divide to one more place than you are rounding to.
Step 2: Round the quotient.
$511.687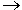 
$511.69
Answer: Dana will make 48 monthly payments of $511.69 each.
In Example 1, we wrote zeros to the right of the decimal point in the dividend ($24,561) without changing the value of that number. We divided to thousandths so that we could round the quotient to the nearest hundredth.When rounding decimal quotients, we must divide to one more place than we are rounding to. The extra digit in the quotient helps us to round up or down. Let's look at some more examples of rounding decimal quotients.
Example 2: Round the quotient of 70.4 and 18 to the nearest tenth.
Step 1: Divide to one more place than you are rounding to.
Step 2: Round the quotient.
3.91 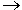3.9
Answer: Rounded to the nearest tenth, the quotient of 70.4 and 18 is 3.9.
Example 3: Round the quotient of 123.7 and 58 to the nearest thousandth.
Step 1: Divide. Write zeros to the right of the last digit in the dividend, if necessary.
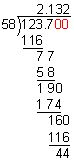
Divide to one more place than you are rounding to.
Step 2: Round the quotient.
2.1327 2.133
Answer: Rounded to the nearest thousandth, the quotient of 123.7 and 58 is 2.133.
You may be wondering when it is necessary to round a quotient. When working with money, we usually round to the nearest cent, as shown in Example 1. Rounding the quotient may also be necessary when finding an average, as shown in Example 4 below.
Example 4: What is the average of these numbers 5.58, 6.02, 3.3? Round your answer to the nearest tenth.
Analysis: We must find the sum of these numbers, divide the sum by 3, then round the quotient to the nearest tenth.
Add:
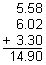
Divide:
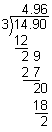
Round: 4.96 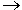5.0
Answer: Rounded to the nearest tenth, the average of 5.58, 6.02 and 3.3 is 5.0.
Example 5: Round the quotient of 15.1 and 3 to the nearest hundredth.
Step 1: Divide. Write zeros to the right of the last digit in the dividend, if necessary.
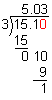
Divide to one more place than you are rounding to.
Step 2: Round the quotient.
5.03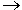3 5.03
Answer: Rounded to the nearest hundredth, the quotient of 15.1 and 3 is 5.03
Example 6: Six cartons of soda cost $45.99. How much does one carton cost? Round your answer to the nearest cent.
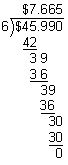
Answer: Rounded to the nearest cent, one carton of soda will cost $7.67.
Example 7: Can 2.4 be rounded to the nearest hundredth? Explain why or why not.
Answer: No. The number 2.4 cannot be rounded to the nearest hundredth because there is no hundredth (or thousandth) digit to use for rounding.
Summary: To round decimal quotients, we use the following procedure:
- Divide.
- Write zeros to the right of the last digit in the dividend, if necessary.
- Divide to one more place than you are rounding to.
- Round the quotient to the designated place.
Exercises
Directions: Read each question below. You may use paper and pencil to help you solve these problems. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. |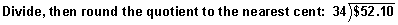 
|
| 2. | 
|
| 3. | 
|
| 4. | 
|
| 5. | What is the average speed in miles per hour if a train traveled 1,912.6 miles in 16 hours? Round your quotient to the nearest hundredth. |
