Example 1: If gasoline costs $6.50 per gallon and your gas tank holds 15.5 gallons, then about how much will you pay to fill your tank?
Analysis: The phrase about how much indicates that we need to estimate. To solve this problem, we will estimate the product of these decimal factors. There are many strategies that we could use. Let's try the two strategies shown below.
Estimates:
Strategy 1: Round both factors to the nearest one.
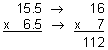
The estimated product is $112.
Strategy 2: Round one factor up and one factor down.
The estimated product is $100.
Answer: Using the first estimation strategy, it will cost about $112 to fill your gas tank. Using the second estimation strategy, it will cost about $100 to to fill your gas tank.
In the example above, the ones digit of each factor is close to 5. The factor 15.5 is about halfway between 10 and 20, and the factor 6.5 is about halfway between 0 and 10. Thus, it is easier to round one factor up and one factor down (10 x 10) than to round each decimal to the nearest one (16 x 7). The actual answer is $100.75, so both estimates are reasonable. However, for this problem, the second strategy was easier to use.
There are other estimation strategies we can use. The compatible numbers strategy makes it easy to do mental arithmetic.
Definition: Compatible numbers are numbers that are close in value to the actual numbers and which make it easy to do mental arithmetic. When estimating with compatible numbers, you generally choose numbers that you can work with mentally.
Example 2: Estimate the product: 46.5 x 2.4
Analysis: If we round each decimal factor to the nearest one, we would get 47 x 2. The factor 46.5 is close to 50 and the factor 2.4 is close to 2. Therefore, choosing compatible numbers 50 and 2 would make it easier to multiply mentally.
Estimate: Strategy 3: Use compatible numbers to estimate the product.
Answer: The estimated product of 46.5 and 2.4 is 100.
In Example 2, each factor was changed to a compatible number. The numbers 50 and 2 are compatible since they make it easy to multiply mentally. So far, we have tried three different strategies for estimating decimal products. Let's look at an example that uses a fourth strategy.
Example 3: Estimate the product: 74.8 x 5.7
Analysis: If we round each decimal factor to the nearest one, we would get 75 x 6. These numbers are not easy to multiply. Let's try another strategy.
Estimate: Strategy 4: Round both factors down and then both factors up
to find a range for the product.
Round both factors down
Round both factors up
Answer: The product of 74.8 and 5.7 ranges from 350 to 480.
Note that in Example 3, we used one strategy that consisted of two parts. We know that the product of 74.8 and 5.7 can be no less than 350 and no more than 480. This is because 70 and 5 are both less than the actual factors and 80 and 6 are both greater than the actual factors. Thus, we can be certain that the product ranges from 350 to 480.
In each of the examples above, rounding a decimal to the nearest one was not the preferred strategy. This is because you can end up with numbers that are not easy to multiply, such as 16 x 7. For the balance of this lesson, we will focus on the following strategies for estimating decimal products:
- Round one factor up and one factor down to estimate the product.
- Use compatible numbers to estimate the product.
- Round both factors down and then both factors up to find a range for the product.
In Examples 4 though 6, we will analyze each problem to determine which of these estimation strategies is easiest to use.
Example 4: Estimate the product: 65.3 x 44.8
Analysis: The ones digit of each factor is close to 5. The factor 65.3 is about halfway between 60 and 70, and the factor 44.8 is about halfway between 40 and 50.
Strategy: Round one factor up and one factor down to estimate the product.
Estimate:
Answer: The estimated product of 65.3 and 44.8 is 2,800.
When we round one factor up and one factor down, we round to the tens place. (If we rounded to the ones place, that would give us 65 x 45, and these numbers are not easy to multiply.)
Example 5: Estimate the product: 53.9 x 32.1
Analysis: The ones digit of each factor is not close to 5, so rounding one factor up and one factor down is not a good strategy for this problem. With compatible numbers, we use numbers such as 50 and 30 to make the arithmetic easy. However, 50 and 30 are both less than the actual factors, so we will get an underestimate. Instead, we will round both factors down and then both factors up to find a range for the product.
Strategy: Round both factors down and then both factors up to find a range for the product.
Estimate: Round both factors down
Round both factors up
Answer: The product of 53.9 and 32.1 ranges from 1,500 to 2,400.
In Example 5, we know that the product of 53.9 and 32.1 can be no less than 1,500 and no more than 2,400. This is because 50 and 30 are both less than the actual factors and 60 and 40 are both greater than the actual factors. Thus, we can be certain that the product ranges from 1,500 to 2,400. The actual answer is 1,730.19, so using this strategy gave us a reasonable estimate. (If we had used compatible numbers 50 and 30, our estimated product would have been 1,500, which is an underestimate.)
Example 6: Estimate the product: 26.4 x 2.7.
Analysis: The factor 26.4 is close to 25 and the factor 2.7 is close to 3.
Strategy: Use compatible numbers to estimate the product.
Estimate:
Answer: The estimated product of 26.4 and 2.7 is 75.
In Example 6, each factor was changed to a compatible number. The numbers 25 and 3 are compatible since they make it easy to multiply mentally.
Example 7: A jar of candy costs $3.25. Eric estimated that he would have to pay $24 for 8 jars. If the actual cost is $26, did he overestimate or underestimate? Explain your answer.
Answer: Eric underestimated because his estimated product of $24 was lower than the actual cost of $26.
Example 8: A blank DVD costs $2.89. Sarah estimated that she would have to pay $18 for 6 DVDs. If the actual cost is $17.34, did she overestimate or underestimate? Explain your answer.
Answer: Sarah overestimated because her estimated product of $18 was higher than the actual cost of $17.34.
Example 9: Ken multiplied 7.8 by 8.3 and got a product of 647.4. Use estimation to determine whether his answer is reasonable or unreasonable. Explain your answer.
Answer: Ken’s answer of 647.4 is unreasonable since 8 x 8 = 64.
Example 10: Jill multiplied 21.4 by 9.6 and got a product of 205.44. Use estimation to determine whether her answer is reasonable or unreasonable. Explain your answer.
Answer: Jill’s answer of 205.44 is reasonable since 20 x 10 = 200.
Summary: In this lesson, we learned how to estimate decimal products using three different strategies. Estimates will vary depending on the strategy used. The goal is use the strategy that gives us a reasonable estimate, and which makes it easy to multiply. We also determined if an estimated product was an overestimate or an underestimate by comparing it with the actual answer. Lastly, we used estimation to determine if an answer was reasonable or unreasonable.
Exercises
Directions: Read each question below. You may use paper and pencil to help you estimate. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
1. |
Gisele was asked to estimate the product of 29.4 and 3.2. Which of the following numbers did she use to get a reasonable estimate and multiply mentally? |
| 2. |
When estimating the product of 5.7 and 34.3, Sandy found a range for the product by rounding both factors down and then both factors up. Use estimation to determine which range below is reasonable. |
| 3. |
You are shopping in a video store and have $48.40 to spend. DVDs cost $7.59 each. Estimate the maximum number of DVDs you could buy. |
| 4. |
Sophia multiplied 2.3 and 60.6 to find the product. Use estimation to determine which of the following answers is reasonable. |
| 5. |
Use estimation to choose the correct product: 38.6 x 9.7 |
