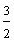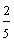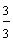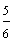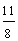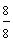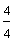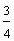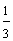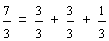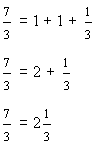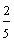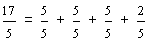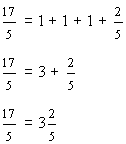Look at each fraction below. How are these fractions similar? How are they different?
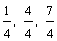
The fractions above are similar since each one has a denominator of 4. Look at the circles below to see how these fractions are different.
1/4 (One-fourth) 4/4 (Four-fourths)
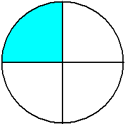
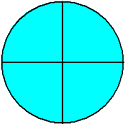
7/4 (Seven-fourths)

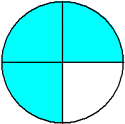
The fraction 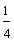 is called a proper fraction. The fractions
is called a proper fraction. The fractions 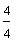 and
and 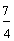 are improper fractions.
are improper fractions.
Definition: A proper fraction is a fraction in which the numerator is less than the denominator.
Definition: An improper fraction is a fraction in which the numerator is greater than or equal to the denominator.
|
In example 1, we will identify each fraction as proper or improper. We will also write each fraction using words.
|
||||||||||||||||||||||||
What do the fractions in example 2 have in common?
Example 2

2/2 (Two-halves)
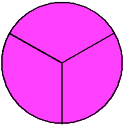
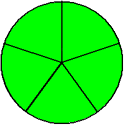
3/3 (Three-thirds)
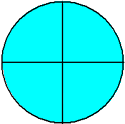
4/4 (Four-fourths)
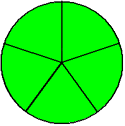
5/5 (Five-fifths)
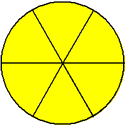
6/6 (Six-sixths)
In example 2, each fraction has a numerator that is equal to its denominator. Each of these fractions is an improper fraction, equal to one whole (1). An improper fraction can also be greater than one whole, as shown in example 3.
Example 3


7/4 (Seven Fourths)
In the improper fraction seven-fourths, the numerator (7) is greater than the denominator (4). We can write this improper fraction as a mixed number.
Definition: A mixed number consists of a whole-number part and a fractional part.
In examples 4 through 6, we will write each improper fraction as a mixed number.
Example 4

 |
 |
|
|
|
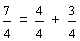 |
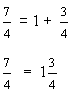 |
In example 4, seven-fourths is an improper fraction. It is really the sum of four-fourths and three-fourths. Seven-fourths is written as the mixed number one and three-fourths, where one is the whole-number part, and three-fourths is the fractional part.
| Example 5 | ||||||||||||||||||
 |
||||||||||||||||||
|
|
|||||||||||||||||
In example 5, the improper fraction seven-thirds is written as the mixed number two and one-third, where two is the whole-number part, and one-third is the fractional part.
| Example 6 | ||||||||
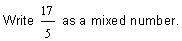 |
||||||||
|
||||||||
|
|
||||||||
|
|
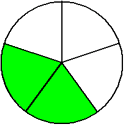
In example 6, the improper fraction seventeen-fifths is written as the mixed number three and two-fifths, where three is the whole-number part, and two-fifths is the fractional part.
In example 7, we will write each number using words. We will then classify each number as a proper fraction, an improper fraction, or a mixed number. Place your mouse over the answer text see if you got it right.
| Example 7 | ||
| Number | Words | Type of Fraction |
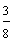 |
three-eighths | answer 1 |
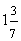 |
one and three-sevenths | answer 2 |
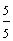 |
five-fifths | answer 3 |
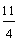 |
eleven-fourths | answer 4 |
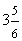 |
three and five-sixths | answer 5 |
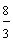 |
eight-thirds | answer 6 |
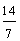 |
fourteen-sevenths | answer 7 |
The last number in example 7 can be written as a whole number: fourteen-sevenths is equal to two wholes (2).
How can you tell if a fraction is less than 1, equal to 1, or greater than 1?
| Compare the numerator and denominator | Example | Type of Fraction | Write As |
| If the numerator < denominator, then the fraction < 1. | 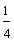 |
proper fraction | proper fraction |
| If the numerator = denominator, then the fraction = 1. | 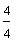 |
improper fraction | whole number |
| If the numerator > denominator, then the fraction > 1. |
|
improper fraction | mixed number |
Summary: A number can be classified as a proper fraction, an improper fraction, or as a mixed number. Any number divided by itself is equal to one. A mixed number consists of a whole-number part and a fractional part.
Exercises
In Exercises 1 through 5, click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR. Note: To write the fraction two-thirds, enter 2/3 into the form.
| 1. | Write a proper fraction using only the digits 7 and 2. |
| 2. | Write an improper fraction using only the digits 5 and 8. |
| 3. | Write twelve-sixths as a whole number. |
| 4. | Write one and two-thirds as an improper fraction. |
| 5. | Write one and one-fourth as an improper fraction. |