Learn About Converting Fractions to Mixed Numbers With Example Problems And Interactive Exercises

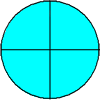
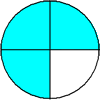
You may recall the example below from a previous lesson.
Example 1![]()
|
|
|
|
|
|
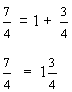 |
In example 1, we used circles to help us solve the problem. Now look at the next example.
 Example 2: At a birthday party, there are 19 cupcakes to be shared equally among 11 guests. What part of the cupcakes will each guest get?
Example 2: At a birthday party, there are 19 cupcakes to be shared equally among 11 guests. What part of the cupcakes will each guest get?
Analysis: We need to divide 19 cupcakes by 11 equal parts. It would be time-consuming to use circles or other shapes to help us solve this problem. Therefore, we need an arithmetic method.
Step 1: Look at the fraction nineteen-elevenths below. Recall that the fraction bar means to divide the numerator by the denominator. This is shown in step 2.
Step 2: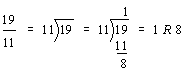
Step 3:
Solution: 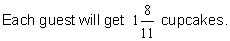
Example 3: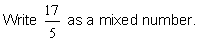
Step 1: 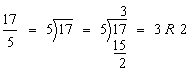
Step 2: 
Answer 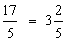
Analysis: We need to divide 37 into 10 equal parts.
Step 1: 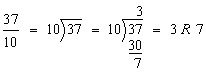
Step 2: ![]()
Answer: ![]()
Example 5: ![]()
Analysis: We need to divide 37 into 13 equal parts.
Step 1: 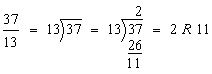
Step 2: ![]()
Answer: ![]()
In each of the examples above, we converted a fraction to a mixed number through long division of its numerator and denominator. Look at example 6 below. What is wrong with this problem?
Example 6: ![]()
Analysis: In the fraction seven-eighths, the numerator is less than the denominator. Therefore, seven-eighths is a proper fraction less than 1. We know from a previous lesson that a mixed number is greater than 1.
Answer: Seven-eighths cannot be written as a mixed number because it is a proper fraction.
Example 7: Can these fractions be written as mixed numbers? Explain why or why not.
![]()
Analysis: In each fraction above, the numerator is equal to the denominator. Therefore, each of these fractions is an improper fraction equal to 1. But a mixed number is greater than 1.
Answer: These fractions cannot be written as mixed numbers since each is an improper fraction equal to 1.
After reading examples 6 and 7, you may be wondering: Which types of fractions can be written as mixed numbers? To answer this question, let's review an important chart from a previous lesson.
Comparison of numerator and denominator: If the numerator < denominator, then the fraction < 1
Example: ![]()
Type of Fraction: proper fraction
Write As: proper fraction
Comparison of numerator and denominator: If the numerator = denominator, then the fraction = 1.
Example: ![]()
Type of Fraction: improper fraction
Write As: whole number
Comparison of numerator and denominator: If the numerator > denominator, then the fraction > 1.
Example: ![]()
Type of Fraction: improper fraction
Write As: mixed number
The answer to the question is: Only an improper fraction greater than 1 can be written to a mixed number.
Summary: We can convert an improper fraction greater than one to a mixed number through long division of its numerator and denominator.
Exercises
In Exercises 1 through 5, click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR. Note: To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.
| 1. | Write eleven-fifths as a mixed number. |
| 2. | Write eleven-fourths as a mixed number. |
| 3. | Write thirteen-ninths as a mixed number. |
| 4. | On field day, there are 23 pies to share equally among 7 classes. What part of the pies will each class get? |
| 5. | A teacher gives her class a spelling test worth 35 points. If there are 8 words graded equally, then how many points is each word worth? |