What Are Fractions: Step by Step Lesson with Interactive Exercises
A circle is a geometric shape that we have seen in other lessons. The circle to the left can be used to represent one whole. We can divide this circle into equal parts as shown below.
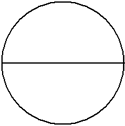
This circle has been divided into 2 equal parts.
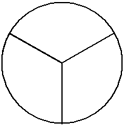
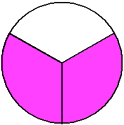
This circle has been divided into 3 equal parts.
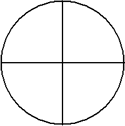
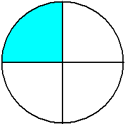
This circle has been divided into 4 equal parts.
We can shade a portion of a circle to name a specific part of the whole as shown below.
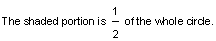
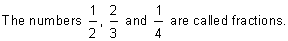
What Are Fractions? Definition: A fraction names part of a region or part of a group. The top number of a fraction is called its numerator and the bottom part is its denominator.
So a fraction is the number of shaded parts divided by the number of equal parts as shown below:
number of shaded parts numerator
number of equal parts denominator
Looking at the numbers above, we have:
There are two equal parts, giving a denominator of 2. One of the parts is shaded, giving a numerator of 1.
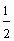
There are three equal parts, giving a denominator of 3. Two of the parts are shaded, giving a numerator of 2.
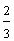
There are four equal parts, giving a denominator of 4. One of the parts is shaded, giving a numerator of 1.
Note that the fraction bar means to divide the numerator by the denominator. Let's look at some more examples of fractions. In examples 1 through 4 below, we have identified the numerator and the denominator for each shaded circle. We have also written each fraction as a number and using words.
Example 1:
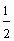
One-half
Example 2:
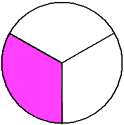
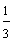
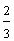
One-third two-thirds
Example 3:
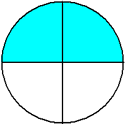
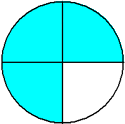
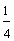
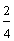
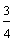
One-fourth Two-fourths Three-fourths
Example 4:
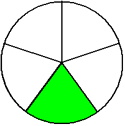
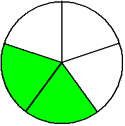
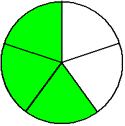
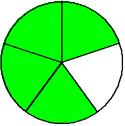
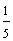
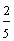
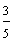
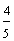
One-fifth Two-fifths Three-fifths Four-fifths
Why is the number 3/4ths written as three-fourths? We use a hyphen to distinguish a fraction from a ratio. For example, "The ratio of girls to boys in a class is 3 to 4." This ratio is written a 3 to 4, or 3:4. We do not know how many students are in the whole class. However, the fraction 3/4 is written as three-fourths (with a hyphen) because 3 is 3/4 of one whole. Thus a ratio names a relationship, whereas, a fraction names a number that represents the part of a whole. When writing a fraction, a hyphen is always used.
It is important to note that other shapes besides a circle can be divided in equal parts. For example, we can let a rectangle represent one whole, and then divide it into equal parts as shown below.
two equal parts
three equal parts
four equal parts
five equal parts
Remember that a fraction is the number of shaded parts divided by the number of equal parts. In the example below, rectangles have been shaded to represent different fractions.
Example 5:
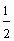One-half
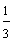One-third
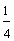One-fourth
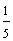One-fifth
The fractions above all have the same numerator. Each of these fractions is called a unit fraction.
Definition: A unit fraction is a fraction whose numerator is one. Each unit fraction is part of one whole (the number 1). The denominator names that part. Every fraction is a multiple of a unit fraction.
In examples 6 through 8, we will identify the fraction represented by the shaded portion of each shape.
Example 6:
In example 6, there are four equal parts in each rectangle. Three sections have been shaded in each rectangle, but not the same three. This was done intentionally to demonstrate that any 3 of the 4 equal parts can be shaded to represent the fraction three-fourths.
A. 
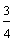
B. 
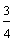
Example 7:
In example 7, each circle is shaded in different sections. However, both circles represent the fraction two-thirds. The value of a fraction is not changed by which sections are shaded.
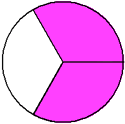
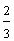
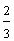
Example 8:
In example 8, each rectangle is shaded in different sections. However, both rectangles represent the fraction two-fifths. Once again, the value of a fraction is not changed by which sections are shaded.
A. 
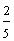
B. 
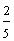
In the examples above, we demonstrated that the value of a fraction is not changed by which sections are shaded. This is because a fraction is the number of shaded parts divided by the number of equal parts.
Let's look at some more examples.
Example 9:
In example 9, the circle has been shaded horizontally; whereas, in example 10, the circle was shaded vertically. The circles in both examples represent the same fraction, one-half. The positioning of the shaded region does not change the value of a fraction.
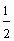
Example 10:
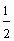
Example 11:
In example 11, the rectangle is positioned horizontally; whereas in example 12, the rectangle is positioned vertically. Both rectangles represent the fraction four-fifths. The positioning of a shape does not change the value of the fraction it represents.
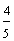
Example 12:
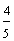
Remember that a fraction is the number of shaded parts divided by the number of equal parts.
In example 13, we will write each fraction using words. Place your mouse over the red text to see if you got it right.
| Example 13 | |
| Number | Words |
 |
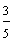answer 1 |
 |
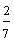answer 2 |
 |
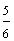answer 3 |
 |
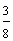answer 4 |
Summary: What Are Fractions? A fraction names part of a region or part of a group. A fraction is the number of shaded parts divided by the number of equal parts. The numerator is the number above the fraction bar, and the denominator is the number below the fraction bar.
Exercises
In Exercises 1 through 5, click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR. Note: To write the fraction two-thirds, enter 2/3 into the form.
| 1. What fraction is represented by the shaded rectangle below? | |
 |
|
| 2. What fraction is represented by the shaded circle below? |
 |
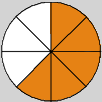| 3. Write one-sixth as a fraction. |
| 4. Write three-sevenths as a fraction. |
| 5. Write seven-eighths as a fraction. |
