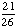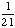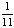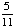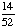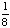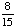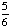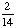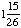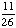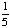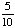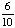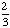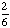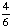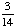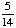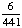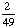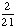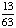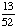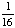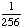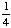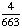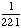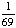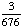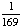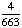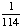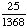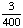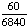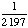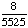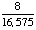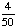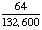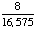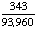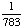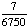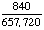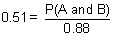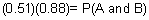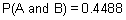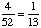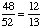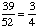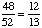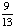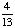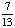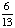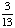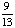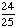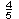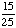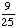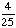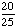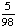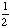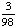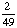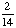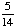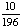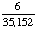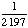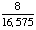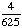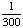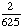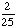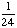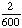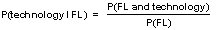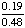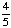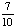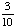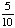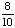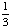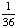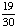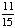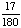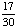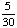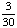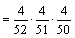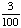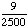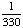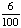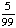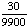Introduction to Probability
| Exercise | Problem | Solution |
| 1 | Which of the following is an experiment?
Tossing a coin. |
All of the above. |
| 2 | Which of the following is an outcome?
Rolling a pair of dice. |
Landing on red. |
| 3 | Which of the following experiments does NOT have equally likely outcomes?
Choose a number at random from 1 to 7. |
Choose a letter at random from the word SCHOOL (SCHOOL has 2 O's). |
| 4 | What is the probability of choosing a vowel from the alphabet?
None of the above. |
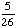 |
| 5 | A number from 1 to 11 is chosen at random. What is the probability of choosing an odd number?
None of the above. |
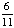 |
Certain and Impossible Events
| Exercise | Problem | Solution |
| 1 | A glass jar contains 5 red, 3 blue and 2 green jelly beans. If a jelly bean is chosen at random from the jar, then which of the following is an impossible event?
Choosing a red jelly bean. |
Choosing a yellow jelly bean. |
| 2 | A spinner has 7 equal sectors numbered 1 to 7. If you spin the spinner, then which of the following is a certain event?
Landing on a number less than 7. |
Landing on a number less than 8 |
| 3 | What is the probability of choosing 14 hearts from a standard deck of 52 playing cards?
1 0 None of the above. |
0; Each suit has only 13 cards. |
| 4 | If a number is chosen at random from the following list, then what is the probability that it is prime? 2, 3, 5, 7, 11, 13, 17, 19 1 0 None of the above. |
1 |
| 5 | If a single 6-sided die is rolled, then which of the following events is neither certain nor impossible?
Rolling a number less than 7. |
Rolling an even number. |
Sample Spaces
| Exercise | Problem | Solution |
| 1 | What is the sample space for choosing an odd number from 1 to 11 at random?
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 |
{1, 3, 5, 7, 9 11} |
| 2 | What is the sample space for choosing a prime number less than 15 at random?
{2, 3, 5, 7, 11, 13, 15} |
{2, 3, 5, 7, 11, 13} |
| 3 | What is the sample space for choosing 1 jelly bean at random from a jar containing 5 red, 7 blue and 2 green jelly beans?
{5, 7, 2} |
{red, blue, green} |
| 4 | What is the sample space for choosing 1 letter at random from 5 vowels?
{a, e, i, o, u} |
{a, e, i, o, u} |
| 5 | What is the sample space for choosing 1 letter at random from the word DIVIDE?
{d, i, v, i, d, e} |
{d, i, v, e} |
The Complement of an Event
| Exercise | Problem | Solution |
| 1 | A glass jar contains 5 red, 3 blue and 2 green jelly beans. If a jelly bean is chosen at random from the jar, what is the probability that it is not blue?
None of the above. |
1 - 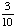 = = 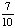 Answer: |
| 2 | A student is chosen at random from a class of 16 girls and 14 boys. What is the probability that the student chosen is not a girl?
1 None of the above. |
1 - 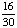 = = 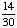 = = 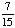 Answer: |
| 3 | A number from 1 to 5 is chosen at random. What is the probability that the number chosen is not odd?
0 None of the above. |
1 - 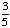 = = 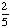 Answer: |
| 4 | If a number is chosen at random from the following list, what is the probability that it is not prime? 2, 3, 5, 7, 11, 13, 17, 19 1 0 None of the above. |
1 - 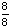 = 0 = 0
Answer: 0 (this is an impossible event) |
| 5 | If a single 6-sided die is rolled, what is the probability of rolling a number that is not 8?
1 0 None of the above. |
P(8) = 0; P(not 8) = 1 - 0 = 1
Answer: 1 (This is a certain event) |
Mutually Exclusive Events
| Exercise | Problem | Solution |
| 1 | Which of the following are mutually exclusive events when a single card is chosen at random from a standard deck of 52 playing cards?
Choosing a 7 or Choosing a club. |
Choosing a 7 or Choosing a jack |
| 2 | All of the following are mutually exclusive events when a single 6-sided die is rolled EXCEPT:
Rolling a number less than 4 or Rolling a number greater than 4. |
Rolling a 2 or Rolling an even number. |
| 3 | Which of the following are mutually exclusive events when a day of the week is chosen at random?
Choosing a Monday or Choosing a Wednesday. |
All of the above. |
| 4 | A single letter is chosen at random from the word TEACHER. All of the following are mutually exclusive events except:
Choosing a T or Choosing a consonant. |
Choosing a T or Choosing a consonant. |
| 5 | Which of the following are mutually exclusive events when a month of the year is chosen at random?
Choosing August or Choosing a summer month. |
Choosing a summer month or Choosing a winter month. |
Addition Rules for Probability
| Exercise | Problem | Solution |
| 1 | A day of the week is chosen at random. What is the probability of choosing a Monday or Tuesday?
None of the above. |
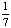 + + 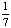 = = 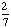 Answer: |
| 2 | In a pet store, there are 6 puppies, 9 kittens, 4 gerbils, and 7 parakeets. If a pet is chosen at random, what is the probability of getting a puppy or a parakeet?
None of the above. |
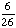 + + 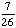 = = 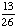 = = 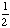 Answer: |
| 3 | The probability of a New York teenager owning a skateboard is 0.37, of owning a bicycle is 0.81, and of owning both is 0.36. If a New York teenager is chosen at random, what is the probability that the teenager owns a skateboard or a bicycle?
1.18 |
(0.37 + 0.81) - 0.36 = 0.82
Answer: 0.82 |
| 4 | A number from 1 to 10 is chosen at random. What is the probability of choosing a 5 or an even number?
All of the above. |
P(5) = 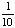 P(even) = P(5 or even) = Answer: |
| 5 | A single 6-sided die is rolled. What is the probability of rolling a number greater than 3 or an even number?
1 None of the above. |
P(greater than 3) = 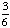 P(even) = P(both) = P(greater than 3 AND even) = ( Answer: |
Probability of Independent Events
| Exercise | Problem | Solution |
| 1 | Spin a spinner numbered 1 to 7, and toss a coin. What is the probability of getting an odd number on the spinner and a tail on the coin?
None of the above. |
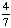 · · 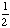 = = 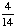 = = 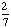 Answer: |
| 2 | A jar contains 6 red balls, 3 green balls, 5 white balls and 7 yellow balls. Two balls are chosen from the jar, with replacement. What is the probability that both balls are green?
None of the above. |
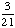 · · 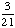 = = 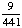 = = 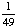 Answer: |
| 3 | In Exercise 2, what is the probability of getting a red and a yellow ball?
All of the above. |
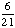 · · 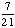 = = 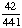 = Answer: |
| 4 | Four cards are chosen from a standard deck of 52 playing cards with replacement. What is the probability of choosing 4 hearts in a row?
None of the above. |
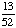 · · 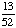 · · 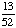 · · 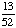 = Answer: |
| 5 | A nationwide survey showed that 65% of all children in the United States dislike eating vegetables. If 4 children are chosen at random, what is the probability that all 4 dislike eating vegetables? (Round your answer to the nearest percent.)
18% |
65% = .65;
(.65)(.65)(.65)(.65) = .179 .179 rounded to the nearest percent is 18% Answer: 18% |
Probability of Dependent Events
| Exercise | Problem | Solution |
| 1 | Two cards are chosen at random from a deck of 52 cards without replacement. What is the probability of getting two kings?
None of the above. |
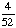 · · 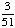 = = 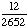 = Answer: |
| 2 | Two cards are chosen at random from a deck of 52 cards without replacement. What is the probability that the first card is a jack and the second card is a ten?
None of the above. |
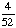 · · 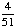 = = 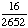 = Answer: |
| 3 | On a math test, 5 out of 20 students got an A. If three students are chosen at random without replacement, what is the probability that all three got an A on the test?
None of the above. |
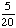 · · 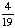 · · 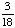 = =
Answer: |
| 4 | Three cards are chosen at random from a deck of 52 cards without replacement. What is the probability of getting an ace, a king and a queen in order?
None of the above. |
P(ace, king, queen)
= Answer: |
| 5 | A school survey found that 7 out of 30 students walk to school. If four students are selected at random without replacement, what is the probability that all four walk to school?
None of the above. |
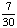 · · 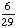 · · 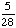 · · 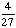 = =
Answer: |
Conditional Probability
| Exercise | Problem | Solution |
| 1 | In New York State, 48% of all teenagers own a skateboard and 39% of all teenagers own a skateboard and rollerblades. What is the probability that a teenager owns rollerblades given that the teenager owns a skateboard?
87% |
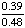 = .8125 = .8125
Answer: 81% (to the nearest percent) |
| 2 | At a middle school, 18% of all students play football and basketball, and 32% of all students play football. What is the probability that a student plays basketball given that the student plays football?
56% |
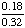 = .5625 = .5625
Answer: 56% (to the nearest percent) |
| 3 | In the United States, 56% of all children get an allowance and 41% of all children get an allowance and do household chores. What is the probability that a child does household chores given that the child gets an allowance?
137% |
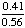 = .7321 = .7321
Answer: 73% (to the nearest percent) |
| 4 | In Europe, 88% of all households have a television. If it is known that 51% of all households have a VCR given that they also have a television, then what is the probability that a household has a VCR and a television?
58% |
Let A denote the event "have a television" and let B denote the event "have a VCR".
Answer: 45% (to the nearest percent) |
| 5 | In New England, 84% of the houses have a garage and 65% of the houses have a garage and a back yard. What is the probability that a house has a backyard given that it has a garage?
77% |
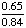 = .7738 = .7738
Answer: 77% (to the nearest percent) |
Practice Exercises
| Exercise | Problem | Solution |
| 1 | Which of the following is an impossible event?
Choosing an odd number from 1 to 10. |
Choosing a white marble from a jar of 25 green marbles. |
| 2 | Which of the following is the sample space for choosing a letter from the word LIBRARY?
{I, A} |
{L, I, B, R, A, Y} |
| 3 | What is the probability that a single card chosen from a deck is not an ace?
None of the above. |
P(not ace) = 1 - P(ace)
= 1 - = Answer: |
| 4 | Which of the following is a certain event?
Choosing a teacher from a room full of students. |
The probability of a certain event is equal to 1.
Answer: None of the above. |
| 5 | There are 4 parents, 3 students and 6 teachers in a room. If a person is selected at random, what is the probability that it is a teacher or a student?
None of the above. |
P(teacher or student) = P(teacher) + P(student)
= = Answer: |
| 6 | In a high school computer class there are 15 juniors and 10 seniors. Four juniors and five seniors are boys. If a student is selected at random, then what is the probability of selecting a junior or a boy?
None of the above. |
P(junior or boy)
= P(junior) + P(boy) - P(junior and boy) = = Answer: |
| 7 | A jar contains 5 red, 3 green, 2 purple and 4 yellow marbles. A marble is chosen at random from the jar. After replacing it, a second marble is chosen. What is the probability of choosing a purple and then a red marble?
|
P(purple, red) = P(purple) · P(red)
= = = Answer: |
| 8 | Three cards are chosen at random from a deck without replacement. What is the probability of choosing an eight, a seven and a six, in order?
None of the above. |
P(eight, seven, six)
= = = Answer: |
| 9 | In a shipment of 25 DVD Players, 2 are defective. If 2 DVD Players are randomly selected and tested, what is the probability that both are defective if the first one is not replaced after it has been tested?
None of the above. |
P(defective, defective)
= = = Answer: |
| 10 | In a school, 48% of the students take a foreign language class and 19% of students take both foreign language and technology. What is the probability that a student takes technology given that the students takes foreign language? (Round your answer to the nearest percent.)
67% |
Let FL represent foreign language
= = 0.3958333... = 40% rounded to the nearest percent Answer: 40% |
Challenge Exercises
| Exercise | Problem | Solution |
| 1 | Which of the following is the sample space when 2 coins are tossed?
{H, T, H, T} |
{HH, HT, TH, TT} |
| 2 | At Kennedy Middle School, 3 out of 5 students make honor roll. What is the probability that a student does not make honor roll?
65% |
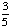 = .60; 1 - .60 = .40 = .60; 1 - .60 = .40
Answer: 40% |
| 3 | A large basket of fruit contains 3 oranges, 2 apples and 5 bananas. If a piece of fruit is chosen at random, what is the probability of getting an orange or a banana?
None of the above. |
P(orange or banana)
= = Answer: |
| 4 | A pair of dice is rolled. What is the probability of getting a sum of 2?
None of the above. |
P(1 and 1) = 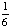 · · 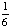 = Answer: |
| 5 | In a class of 30 students, there are 17 girls and 13 boys. Five are A students, and three of these students are girls. If a student is chosen at random, what is the probability of choosing a girl or an A student?
None of the above. |
P(girl) + P(A) - P(girls and A)
= = Answer: |
| 6 | In the United States, 43% of people wear a seat belt while driving. If two people are chosen at random, what is the probability that both of them wear a seat belt?
86% |
(.43)(.43) = .1849
Answer: 18% (to the nearest percent) |
| 7 | Three cards are chosen at random from a deck without replacement. What is the probability of getting a jack, a ten and a nine in order?
None of the above. |
P(jack, ten, nine)
Answer: |
| 8 | A city survey found that 25% of teenagers have a part time job. The same survey found that 40% plan to attend college. If a teenager is chosen at random, what is the probability that the teenager has a part time job and plans to attend college?
65% |
(.25)(.40) = .10
Answer: 10% |
| 9 | In a school, 14% of students take drama and computer classes, and 67% take drama class. What is the probability that a student takes computer class given that the student takes drama class?
81% |
Answer: 21% (to the nearest percent) |
| 10 | In a shipment of 100 televisions, 6 are defective. If a person buys two televisions from that shipment, what is the probability that both are defective?
None of the above. |
P(defective, defective)
= = = Answer: |