Learn About Divisibility Rules With Example Problems And Interactive Exercises
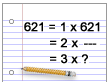 Problem: Is the number 621 prime or composite?
Problem: Is the number 621 prime or composite?
Method: In the last lesson, we learned to find all factors of a whole number to determine if it is prime or composite. We used the procedure listed below.
To determine if a number is prime or composite, follow these steps:
- Find all factors of the number.
- If the number has only two factors, 1 and itself, then it is prime.
- If the number has more than two factors, then it is composite.
The above procedure works very well for small numbers. However, it would be time-consuming to find all factors of 621. Thus we need a better method for determining if a large number is prime or composite. Every number has one and itself as a factor. Thus, if we could find one factor of 621, other than 1 and itself, we could prove that 621 is composite. One way to find factors of large numbers quickly is to use tests for divisibility.
| Definition | Example |
| One whole number is divisible by another if, after dividing, the remainder is zero. | 18 is divisible by 9 since 18 ÷ 9 = 2 with a remainder of 0. |
| If one whole number is divisible by another number, then the second number is a factor of the first number. | Since 18 is divisible by 9, 9 is a factor of 18. |
| A divisibility test is a rule for determining whether one whole number is divisible by another. It is a quick way to find factors of large numbers. | Divisibility Test for 3: if the sum of the digits of a number is divisible by 3, then the number is divisible by 3. |
We can test for divisibility by 3 (see table above) to quickly find a factor of 621 other than 1 and itself. The sum of the digits of 621 is 6+2+1 = 9. This divisibility test and the definitions above tell us that...
- 621 is divisible by 3 since the sum of its digits (9) is divisible by 3.
- Since 621 is divisible by 3, 3 is a factor of 621.
- Since the factors of 621 include 1, 3 and 621, we have proven that 621 has more than two factors.
- Since 621 has more than 2 factors, we have proven that it is composite.
Let's look at some other tests for divisibility and examples of each.
| Divisibility Tests | Example |
| A number is divisible by 2 if the last digit is 0, 2, 4, 6 or 8. | 168 is divisible by 2 since the last digit is 8. |
| A number is divisible by 3 if the sum of the digits is divisible by 3. | 168 is divisible by 3 since the sum of the digits is 15 (1+6+8=15), and 15 is divisible by 3. |
| A number is divisible by 4 if the number formed by the last two digits is divisible by 4. | 316 is divisible by 4 since 16 is divisible by 4. |
| A number is divisible by 5 if the last digit is either 0 or 5. | 195 is divisible by 5 since the last digit is 5. |
| A number is divisible by 6 if it is divisible by 2 AND it is divisible by 3. | 168 is divisible by 6 since it is divisible by 2 AND it is divisible by 3. |
| A number is divisible by 8 if the number formed by the last three digits is divisible by 8. | 7,120 is divisible by 8 since 120 is divisible by 8. |
| A number is divisible by 9 if the sum of the digits is divisible by 9. | 549 is divisible by 9 since the sum of the digits is 18 (5+4+9=18), and 18 is divisible by 9. |
| A number is divisible by 10 if the last digit is 0. |
1,470 is divisible by 10 since the last digit is 0. |
Let's look at some examples in which we test the divisibility of a single whole number.
Example 1: Determine whether 150 is divisible by 2, 3, 4, 5, 6, 9 and 10.
150 is divisible by 2 since the last digit is 0.
150 is divisible by 3 since the sum of the digits is 6 (1+5+0 = 6), and 6 is divisible by 3.
150 is not divisible by 4 since 50 is not divisible by 4.
150 is divisible by 5 since the last digit is 0.
150 is divisible by 6 since it is divisible by 2 AND by 3.
150 is not divisible by 9 since the sum of the digits is 6, and 6 is not divisible by 9.
150 is divisible by 10 since the last digit is 0.
Solution: 150 is divisible by 2, 3, 5, 6, and 10. 
Example 2: Determine whether 225 is divisible by 2, 3, 4, 5, 6, 9 and 10.
225 is not divisible by 2 since the last digit is not 0, 2, 4, 6 or 8.
225 is divisible by 3 since the sum of the digits is 9, and 9 is divisible by 3.
225 is not divisible by 4 since 25 is not divisible by 4.
225 is divisible by 5 since the last digit is 5.
225 is not divisible by 6 since it is not divisible by both 2 and 3.
225 is divisible by 9 since the sum of the digits is 9, and 9 is divisible by 9.
225 is not divisible by 10 since the last digit is not 0.
Solution: 225 is divisible by 3, 5 and 9. 
Example 3: Determine whether 7,168 is divisible by 2, 3, 4, 5, 6, 8, 9 and 10.
7,168 is divisible by 2 since the last digit is 8.
7,168 is not divisible by 3 since the sum of the digits is 22, and 22 is not divisible by 3.
7,168 is divisible by 4 since 168 is divisible by 4.
7,168 is not divisible by 5 since the last digit is not 0 or 5.
7,168 is not divisible by 6 since it is not divisible by both 2 and 3.
7,168 is divisible by 8 since the last 3 digits are 168, and 168 is divisible by 8.
7,168 is not divisible by 9 since the sum of the digits is 22, and 22 is not divisible by 9.
7,168 is not divisible by 10 since the last digit is not 0 or 5.
Solution: 7,168 is divisible by 2, 4 and 8. 
Example 4: Determine whether 9,042 is divisible by 2, 3, 4, 5, 6, 8, 9 and 10.
9,042 is divisible by 2 since the last digit is 2.
9,042 is divisible by 3 since the sum of the digits is 15, and 15 is divisible by 3.
9,042 is not divisible by 4 since 42 is not divisible by 4.
9,042 is not divisible by 5 since the last digit is not 0 or 5.
9,042 is divisible by 6 since it is divisible by both 2 and 3.
9,042 is not divisible by 8 since the last 3 digits are 042, and 42 is not divisible by 8.
9,042 is not divisible by 9 since the sum of the digits is 15, and 15 is not divisible by 9.
9,042 is not divisible by 10 since the last digit is not 0 or 5.
Solution: 9,042 is divisible by 2, 3 and 6. 
Example 5: Determine whether 35,120 is divisible by 2, 3, 4, 5, 6, 8, 9 and 10.
35,120 is divisible by 2 since the last digit is 0.
35,120 is not divisible by 3 since the sum of the digits is 11, and 11 is not divisible by 3.
35,120 is divisible by 4 since 20 is divisible by 4.
35,120 is divisible by 5 since the last digit is 0.
35,120 is not divisible by 6 since it is not divisible by both 2 and 3.
35,120 is divisible by 8 since the last 3 digits are 120, and 120 is divisible by 8.
35,120 is not divisible by 9 since the sum of the digits is 11, and 11 is not divisible by 9.
35,120 is divisible by 10 since the last digit is 0.
Solution: 35,120 is divisible by 2, 4, 5, 8 and 10. 
Example 6: Is the number 91 prime or composite? Use divisibility when possible to find your answer.
91 is not divisible by 2 since the last digit is not 0, 2, 4, 6 or 8.
91 is not divisible by 3 since the sum of the digits (9+1=10) is not divisible by 3.
91 is not evenly divisible by 4 (remainder is 3).
91 is not divisible by 5 since the last digit is not 0 or 5.
91 is not divisible by 6 since it is not divisible by both 2 and 3.
91 divided by 7 is 13.
Solution: The number 91 is divisible by 1, 7, 13 and 91. Therefore 91 is composite since it has more than two factors.
Summary: Divisibility tests can be used to find factors of large whole numbers quickly, and thus determine if they are prime or composite. When working with large whole numbers, tests for divisibility are more efficient than the traditional factoring method.
Exercises
Directions: Read each question below. Select your answer by clicking on the corresponding button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. | The number 477 is divisible by each of the following numbers EXCEPT: 3, 6, 9 |
| 2. | The number 348 is divisible by each of the following numbers EXCEPT: 2, 3, 4, 5, 6 |
| 3. | If a number is divisible by 9, then it is also divisible by which number? |
| 4. | Which number is divisible by 8? |
| 5. | Which number is divisible by 6? |




