 Example 1: What do you notice about each sentence below?
Example 1: What do you notice about each sentence below?
| 1. | A number is even or a number is not even. |
| 2. | Cheryl passes math or Cheryl does not pass math. |
| 3. | It is raining or it is not raining. |
| 4. | A triangle is isosceles or a triangle is not isosceles. |
Each sentence in Example 1 is the disjunction of a statement and its negation Each of these sentences can be written in symbolic form as p ~p. Recall that a disjunction is false if and only if both statements are false; otherwise it is true. By this definition, p
~p. Recall that a disjunction is false if and only if both statements are false; otherwise it is true. By this definition, p ~p is always true, even when statement p is false or statement ~p is false! This is illustrated in the truth table below:
~p is always true, even when statement p is false or statement ~p is false! This is illustrated in the truth table below:
| p | ~p | p ~p ~p |
| T | F | T |
| F | T | T |
The compound statement p ~p consists of the individual statements p and ~p. In the truth table above, p
~p consists of the individual statements p and ~p. In the truth table above, p ~p is always true, regardless of the truth value of the individual statements. Therefore, we conclude that p
~p is always true, regardless of the truth value of the individual statements. Therefore, we conclude that p ~p is a tautology.
~p is a tautology.
Definition: A compound statement, that is always true regardless of the truth value of the individual statements, is defined to be a tautology.
Let's look at another example of a tautology.
Example 2: Is (p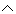 q)
q) p a tautology?
p a tautology?
| p | q | p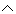 q q |
(p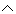 q) q) p p |
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
Solution: The compound statement (p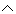 q)
q) p consists of the individual statements p, q, and p
p consists of the individual statements p, q, and p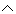 q. The truth table above shows that (p
q. The truth table above shows that (p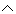 q)
q) p is true regardless of the truth value of the individual statements. Therefore, (p
p is true regardless of the truth value of the individual statements. Therefore, (p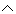 q)
q) p is a tautology.
p is a tautology.
In the examples below, we will determine whether the given statement is a tautology by creating a truth table.
Example 3: Is x (x
(x y) a tautology?
y) a tautology?
| x | y | x y y |
x (x (x y) y) |
| T | T | T | T |
| T | F | T | T |
| F | T | T | T |
| F | F | F | T |
Solution: Yes; the truth values of x (x
(x y) are {T, T, T, T}.
y) are {T, T, T, T}.
Example 4: Is ~b b a tautology?
b a tautology?
| b | ~b | ~b b b |
| T | F | T |
| F | T | F |
Solution: No; the truth values of ~b b are {T, F}.
b are {T, F}.
Example 5: Is (p q)
q) (p
(p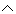 q) a tautology?
q) a tautology?
| p | q | (p q) q) |
(p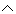 q) q) |
(p q) q) (p (p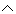 q) q) |
| T | T | T | T | T |
| T | F | T | F | F |
| F | T | T | F | F |
| F | F | F | F | T |
Solution: No; the truth values of (p q)
q) (p
(p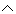 q) are {T, F, F, T}.
q) are {T, F, F, T}.
Example 6: Is [(p q)
q)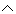 p]
p] p a tautology?
p a tautology?
| p | q | p q q |
(p q) q)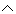 p p |
[(p q) q)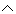 p] p] p p |
| T | T | T | T | T |
| T | F | F | F | T |
| F | T | T | F | T |
| F | F | T | F | T |
Solution: Yes; the truth values of [(p q)
q)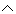 p]
p] p are {T, T, T, T}.
p are {T, T, T, T}.
Example 7: Is (r s)
s)![]() (s
(s r) a tautology?
r) a tautology?
| r | s | r s s |
s r r |
(r s) s) r) r) |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |
Solution: No; the truth values of (r s)
s)![]() (s
(s r) are {T, F, F, T}.
r) are {T, F, F, T}.
 Summary: A compound statement that is always true, regardless of the truth value of the individual statements, is defined to be a tautology. We can construct a truth table to determine if a compound statement is a tautology.
Summary: A compound statement that is always true, regardless of the truth value of the individual statements, is defined to be a tautology. We can construct a truth table to determine if a compound statement is a tautology.
Exercises
Directions: Read each question below. Create a truth table on paper to help you answer each question. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. | What is the truth value of r ~r? ~r? |
| 2. | Is the following statement a tautology? s ~s ~s |
| 3. | Is the following statement a tautology? [(p q) q)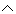 ~p] ~p] q q |
| 4. | Is the following statement a tautology? ~(x y) y) ~y) ~y) |
| 5. | Is the following statement a tautology? a ~a ~a |




