Problem: The mean of 29 test scores is 77.8. What is the sum of these test scores?
Solution: To find the mean of n numbers, we divide the sum of the n numbers by n.
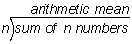
If we let n = 29, we can work backwards to find the sum of these test scores.
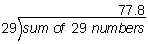
Multiplying the mean by the 29 we get: 77.8 x 29 = 2,256.2
Answer: The sum of these test scores is 2,256.2
In the problem above, we found the sum given the mean and the number of items in the data set (n). It is also possible to find the number of items in the data set (n) given the mean and the sum of the data. This is illustrated in Examples 1 and 2 below.
Example 1: The mean of a set of numbers is 54. The sum of the numbers is 1,350. How many numbers are in the set?
Solution:
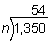
To find n, we need to divide 1,350 by 54.
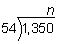
Answer: n = 25, so there are 25 numbers in the set.
Example 2: The mean of a set of numbers is 0.39. The sum of the numbers is 1.56. How many numbers are in the set?
Solution:
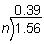
To find n, we need to divide 1.56 by 0.39.
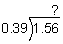
However, we cannot divide by a decimal divisor. We will multiply both the divisor and the dividend by 100 in order to get a whole number divisor.
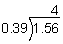
Answer: n = 4, so there are 4 numbers in the set.
In the next few examples, we will be asked to find the missing number in the data set given the other numbers in the data set and the mean. The words mean and average will be used interchangeably.
Example 3: Gini's test scores are 95, 82, 76, and 88. What score must she get on the fifth test in order to achieve an average of 84 on all five tests?
Solution: We are given four of the five test scores. The sum of these 4 test scores is 341. If we let x represent the fifth test score, then the expression 341 + x can represent the sum of all five test scores.
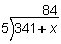
If we multiply the divisor by the quotient, we get:
5 · 84 = 341 + x
420 = 341 + x
420 - 341 = x
x = 79
Answer: Gini needs a score of 79 on her fifth test in order to achieve an average of 84 on all 5 tests.
Example 4: The Lachance family must drive an average of 250 miles per day to complete their vacation on time. On the first five days, they travel 220 miles, 300 miles, 210 miles, 275 miles and 240 miles. How many miles must they travel on the sixth day in order to finish their vacation on time?
Solution: The sum of the first 5 days is 1,245 miles. Let x represent the number of miles traveled on the sixth day. We get:
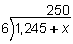
If we multiply the divisor by the quotient, we get:
250 · 6 = 1,245 + x
1,500 = 1,245 + x
1,500 - 1,245 = x
x = 255
Answer: The Lachance family must drive 255 miles on the sixth day in order to finish their vacation on time.
Summary: To find the mean of n numbers, we divide the sum of the n numbers by n.
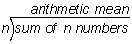
In this lesson, we learned how to solve non-routine problems involving the mean of a set of data. We found the sum given the mean and the number of items in the data set. We also found the number of items in the data set given the mean and the sum of the data. Lastly, we found the missing number in a set of data given the other numbers in the data set and the mean.
Exercises
Directions: Solve each problem using your knowledge of the arithmetic mean. Click once in an ANSWER BOX and type in your answer; then click ENTER. Do not include commas in your answers. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. | The mean of 5 hourly wages is $5.95. What is the sum of these wages? |
| 2. | The mean of a set of numbers is 123. The sum of the numbers is 2,214. How many numbers are in the set? |
| 3. | Laura's math test grades are 87, 93, 89 and 85. What grade must she get on the fifth test in order to get a mean of 90 for the term? |
| 4. | A small company has a limited budget for salaries. It can afford to pay an average of $35,000 a year to its employees. If the first 5 employees are paid $37,000, $38,000, $33,000, $39,000 and $29,000, then how much money can they pay the sixth employee without exceeding their budget? |
| 5. | In problem 4, what would the mean salary be if the sixth was paid $40,000? |
