Practice Exercises for Understanding Percent

Search form

Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.

1.  Which of the following is equal to 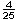four_25ths_2.gif?
 
      4%
      16%
      25%
      None of the above.

      RESULTS BOX:
          
2.  Which of the following is equal to 0.218 ?
 
      .218%
      2.18%
      21.8%
      None of the above.

      RESULTS BOX:
          
3.  Which of the following is equal to 95% ?
 
      

      nineteen_20ths_2.gif

      eighteen_20ths_2.gif

      eighteen_25ths_3.gif

      None of the above.

      RESULTS BOX:
          
4.  Which of the following is equal to 12.5% ?
 
      125
      12.5
      1.25
      None of the above.

      RESULTS BOX:
          
5.  Which of the following is equal to 62.5% ?
 
      

      five_8ths_1.gif

      one_eighth_2.gif

      six_25ths_1.gif

      None of the above.

      RESULTS BOX:
          
6.  Which of the following is equal to 1.75 ?
 
      1.75%
      17.5%
      175%
      None of the above.

      RESULTS BOX:
          
7.  Which of the following is equal to 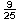nine_25ths_2.gif?
 
      

      thirty6_hundredths_2.gif

      0.36

      36%

      All of the above.

      RESULTS BOX:
          
8.  Which of the following is equal to 0.0947 ?
 
      94.7%
      9.47%
      0.974%
      None of the above.

      RESULTS BOX:
          
9.  Which of the following is equal to 279% ?
 
      2.79
      27.9
      279
      None of the above.

      RESULTS BOX:
          
10.  Which of the following is equal to 0.9625% ?
 
      

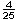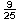      seven_8ths_1.gif

      twenty7_40ths_2.gif

      seventy7_80ths_1.gif

      None of the above.

      RESULTS BOX:
          
Understanding Percent Lessons
Meaning of Percent
Writing Fractions as Percents
Writing Decimals as Percents
Writing Percents as Decimals
Writing Percents as Fractions
Percents < 1 or > 100
Practice Exercises
Challenge Exercises
Solutions

IXL