
 A circle is an important shape in the field of geometry. Let's look at the definition of a circle and its parts. We will also examine the relationship between the circle and the plane.
A circle is an important shape in the field of geometry. Let's look at the definition of a circle and its parts. We will also examine the relationship between the circle and the plane.
A circle is a shape with all points the same distance from its center. A circle is named by its center. Thus, the circle to the right is called circle A since its center is at point A. Some real world examples of a circle are a wheel, a dinner plate and (the surface of) a coin.
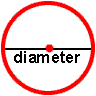 The distance across a circle through the center is called the diameter. A real-world example of diameter is a 9-inch plate.
The distance across a circle through the center is called the diameter. A real-world example of diameter is a 9-inch plate.
 The radius of a circle is the distance from the center of a circle to any point on the circle. If you place two radii end-to-end in a circle, you would have the same length as one diameter. Thus, the diameter of a circle is twice as long as the radius.
The radius of a circle is the distance from the center of a circle to any point on the circle. If you place two radii end-to-end in a circle, you would have the same length as one diameter. Thus, the diameter of a circle is twice as long as the radius.
 We can look at a pizza pie to find real-world examples of diameter and radius. Look at the pizza to the right which has been sliced into 8 equal parts through its center. A radius is formed by making a straight cut from the center to a point on the circle. A straight cut made from a point on the circle, continuing through its center to another point on the circle, is a diameter. As you can see, a circle has many different radii and diameters, each passing through its center.
We can look at a pizza pie to find real-world examples of diameter and radius. Look at the pizza to the right which has been sliced into 8 equal parts through its center. A radius is formed by making a straight cut from the center to a point on the circle. A straight cut made from a point on the circle, continuing through its center to another point on the circle, is a diameter. As you can see, a circle has many different radii and diameters, each passing through its center.
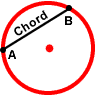 A chord is a line segment that joins two points on a curve. In geometry, a chord is often used to describe a line segment joining two endpoints that lie on a circle. The circle to the right contains chord AB. If this circle was a pizza pie, you could cut off a piece of pizza along chord AB. By cutting along chord AB, you are cutting off a segment of pizza that includes this chord.
A chord is a line segment that joins two points on a curve. In geometry, a chord is often used to describe a line segment joining two endpoints that lie on a circle. The circle to the right contains chord AB. If this circle was a pizza pie, you could cut off a piece of pizza along chord AB. By cutting along chord AB, you are cutting off a segment of pizza that includes this chord.
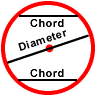 It turns out that a diameter of a circle is the longest chord of that circle since it passes through the center. A diameter satisfies the definition of a chord, however, a chord is not necessarily a diameter. This is because every diameter passes through the center of a circle, but some chords do not pass through the center. Thus, it can be stated, every diameter is a chord, but not every chord is a diameter.
It turns out that a diameter of a circle is the longest chord of that circle since it passes through the center. A diameter satisfies the definition of a chord, however, a chord is not necessarily a diameter. This is because every diameter passes through the center of a circle, but some chords do not pass through the center. Thus, it can be stated, every diameter is a chord, but not every chord is a diameter.
 Let's revisit the definition of a circle. A circle is the set of points that are equidistant from a special point in the plane. The special point is the center. In the circle to the right, the center is point A. Thus we have circle A.
Let's revisit the definition of a circle. A circle is the set of points that are equidistant from a special point in the plane. The special point is the center. In the circle to the right, the center is point A. Thus we have circle A.
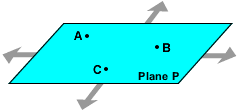
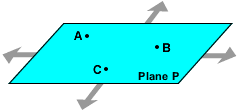 A plane is a flat surface that extends without end in all directions. In the diagram to the right, Plane P contains points A, B and C.
A plane is a flat surface that extends without end in all directions. In the diagram to the right, Plane P contains points A, B and C.
 Can you think of some real world objects that satisfy the definition of a plane? At this level of mathematics, that is difficult to do. Intuitively, a plane may be visualized as a flat infinite sheet of paper. The top of your desk and a chalkboard are objects which can be used to represent a plane, although they do not satisfy the definition above.
Can you think of some real world objects that satisfy the definition of a plane? At this level of mathematics, that is difficult to do. Intuitively, a plane may be visualized as a flat infinite sheet of paper. The top of your desk and a chalkboard are objects which can be used to represent a plane, although they do not satisfy the definition above.
A circle divides the plane into three parts:
- the points INSIDE the circle
- the points OUTSIDE the circle
- and the points ON the circle
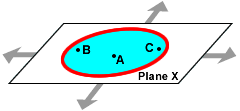
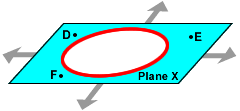
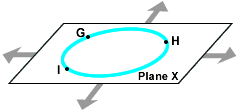
You can see an interactive demonstration of this by placing your mouse over the three items below.
A circle divides a plane into three parts:
 the points INSIDE the circle
the points INSIDE the circle 
- the points OUTSIDE the circle

- and the points ON the circle

 Example 1:
Example 1:
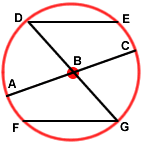
Name the center of this circle.
Answer: Point B
 Example 2:
Example 2:
Name two chords on this circle that are not diameters.
Answer: DE and FG
 Example 3:
Example 3:
Name all radii on this circle.
Answer: BA, BC, BD and BG
 Example 4:
Example 4:
What are AC and DG?
Answer: AC and DG are diameters.
 Example 5:
Example 5:
If DG is 5 inches long, then how long is DB?
Solution: The diameter of a circle is twice as long as the radius.
5 inches ÷ 2 = 2.5 inches
Answer: The length of DB is 2.5 inches
Summary: A circle is a shape with all points the same distance from its center. A circle is named by its center. The parts of a circle include a radius, diameter and a chord. All diameters are chords, but not all chords are diameters. A plane is a flat surface that extends without end in all directions. A circle divides the plane into three parts: The points inside the circle, the points outside the circle and the points on the circle.
1. Which of the following is a chord, but not a diameter?
![]()
![]() 2. Which of the following is a radius?
2. Which of the following is a radius?
![]()

![]() 3. Name the center of this circle.
3. Name the center of this circle.
![]()

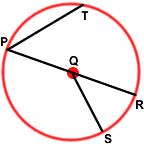
![]() 4. What is PR (or PQR)?
4. What is PR (or PQR)?
![]()

![]() 5. If PQ is 3 cm long, then how long is PR?
5. If PQ is 3 cm long, then how long is PR?
![]()





