 Example 1: Tyrone had a chocolate bar, of which he gave one-half to his friend Nora. Nora gave one-half of her piece to her friend Eduardo. What fractional part of the original chocolate bar did Eduardo get?
Example 1: Tyrone had a chocolate bar, of which he gave one-half to his friend Nora. Nora gave one-half of her piece to her friend Eduardo. What fractional part of the original chocolate bar did Eduardo get?
Analysis: We are taking part of a part. So we must end up with an even smaller part. The word OF means "times", which indicates that we need to multiply.
Solution: One-half of one whole is one-half. One-half of one-half is one-fourth.
Step 1:

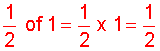
Step 2:

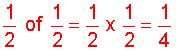
The solution above should make sense given our knowledge of fractions. We also can check this solution using our knowledge of decimals as follows:
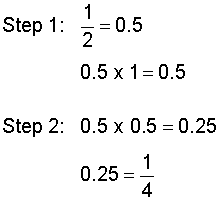
Let's look at another example.
 Example 2: Estelle had a chocolate bar, of which she gave one-half to her friend Lourdes. Lourdes gave two-thirds of her piece to her friend Donna. What fractional part of the original chocolate bar did Donna get?
Example 2: Estelle had a chocolate bar, of which she gave one-half to her friend Lourdes. Lourdes gave two-thirds of her piece to her friend Donna. What fractional part of the original chocolate bar did Donna get?
Analysis: The word OF means "times". We will multiply one-half by two-thirds.
Solution: We can show the solution in three steps.
Step 1:

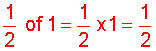
Step 2:

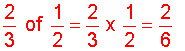
Step 3:

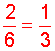
Answer: Donna got one-third of the original chocolate bar.
The original chocolate bar consisted of 6 sections. Estelle gave Lourdes one-half of those, which is 3 sections. Lourdes gave Donna two-thirds of those, which is 2 sections. As you can see, 2 sections is one-third of 6. This leads us to the following procedure for multiplying fractions.
Procedure: To multiply two fractions:
- Multiply the numerators by the numerators
- Multiply the denominators by the denominators
- Simplify your result, if necessary.
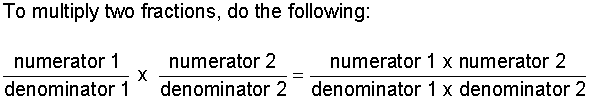
Let's look at some examples of multiplying fractions using this procedure.
Example 3: Multiply
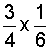
Analysis: We will multiply two fractions.
Solution:
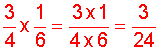
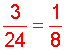
Recall that the best way to simplify a fraction (reduce a fraction to lowest terms) is to find the greatest common factor of it's numerator and denominator; then divide both the numerator and the denominator by that same (nonzero) whole number.
Example 4: Multiply
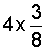
Analysis: We will multiply a whole number by a fraction. Since 4 over 1 is the same as 4, we get.
Solution:
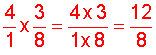
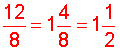
In example 4, the GCF of 12 and 8 is 4. We could have simplified the result by cancelling (dividing out) a common factor of 4. This is shown below:
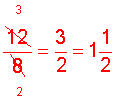
Example 5: Multiply
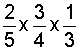
Analysis: We will multiply three fractions.
Solution:
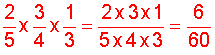
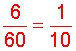
Example 6: One batch of muffins contains 3/4 cups of raisins. How many cups of raisins are needed to make 6 batches of muffins?
Analysis: We will multiply a fraction by a whole number.
Solution:
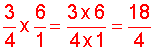
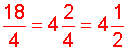
We need 4 and 1/2 cups of raisins to make 5 batches of muffins.
Example 7: Multiply.
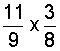
Analysis: We will multiply an improper fraction by a proper fraction.
Solution:
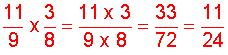
Summary: To multiply two or more fractions, multiply the numerators together and then multiply the denominators together. Simplify your result, if necessary.
Exercises
Directions: Multiply the fractions in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
Note: To write the fraction three-fourths, enter 3/4 into the form. To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.
| 1. | 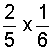 |
| 2. | 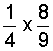 |
| 3. | 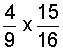 |
| 4. | 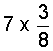 |
| 5. | If it takes 2/5 meters of fabric to make a blouse, then how many meters will it take to make 9 blouses? |




