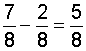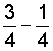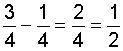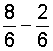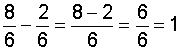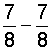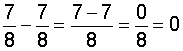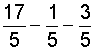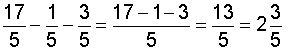Lesson on Subtracting Fractions with Like Denominators

Example 1:  Nick was at a party and saw a pizza divided into eight equal parts (slices). By the time he got to the food table, only 7 slices of pizza were there. If Nick ate 2 of those slices, then what part of the pizza was left for other guests to eat? Analysis: We need to find the difference between 7 eighths and 2 eighths. The denominator of a fraction names the unit. The numerator indicates how many there are. Solution:   Five-eighths of the pizza was left for other guests to eat.

In the last lesson, we learned how to add fractions with a common denominator. It works the same way for subtracting fractions. In order to subtract fractions, the denominators must be the same -- they must have a common denominator.

This leads us to the following procedure for subtracting fractions with a common denominator.

Procedure: To subtract two or more fractions that have the same denominators, subtract the numerators and place the resulting difference over the common denominator. Simplify your result, if necessary.

Applying this procedure to example 1, we get:

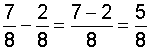
Let's look at some examples of subtracting fractions using this procedure.

Example 2:  Analysis: Subtract the numerators and place the difference over the common denominator, 4. Solution:

In example 2, we needed to simplify the result: We reduced two-fourths to lowest terms.

Example 3:  Analysis: Subtract the numerators and place the difference over the common denominator, 6. Solution:

In example 4, we simplified the result by converting the improper fraction to a mixed number. Then we reduced the fractional part of the mixed number to lowest terms.

Avoid This Common Mistake!

Recall that a fraction bar separates the numerator and denominator of a fraction. It indicates that a division of the numerator by the denominator will be performed.  It is mathematically incorrect to subtract the denominators as well as the numerators. To see why this is wrong, look at the example below.

Example 5: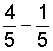
Analysis:	Subtracting the numerators and mistakenly subtracting the denominators produces this result:
Result: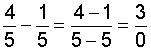
Explanation:	We end up with zero in the denominator of our result. This means that we need to divide by zero. But division by zero is undefined!

To understand why division by zero is undefined, let's look at the relationship between multiplication and division. If x is any number, then:

The Multiplication Property of Zero states that the product of zero and any number is zero. Since 0 times any number is 0, there is no value of x that would make this last statement true. Therefore, division by zero is undefined, and we do not subtract denominators!

Since division by zero is undefined, you can see why the definition of a fraction specifies a nonzero denominator, as follows:

Let's look at some more examples:

Example 6:  Analysis: If there are 7 slices of pizza on a plate, and 7 are eaten, then there are no (0) slices left. Solution:

In example 6, both fractions have the same numerator. Subtracting the numerators, we get 7 minus 7 is 0. This makes sense since any number minus itself is equal to zero. When we place this difference over the common denominator, our result is 0 eighths. However, you may be wondering why 0 eighths is equal to 0. Remember that the denominator of a fraction names the unit, and the numerator indicates how many there. So if we have 0 eighths, then that is just plain 0. In short, we simplified the result to zero. Look at examples 7 through 9 below.

Example	Problem	Subtract	Simplify
7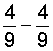
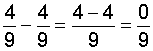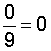8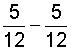
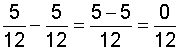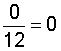9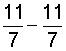

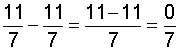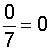In each example above, we simplified the result to zero through division of the numerator (0) by the denominator. Recall that the fraction bar tells us to divide the numerator by the denominator, and zero divided by any nonzero number is zero. Therefore, any fraction with zero in the numerator and a nonzero number in the denominator equals zero. This is summarized below.

So far, we have subtracted only two fractions at a time. We can subtract more than two fractions using the procedure above. This is shown in example 10.

Example 10:  Analysis: Subtract the numerators and place the difference over the common denominator, 5. Solution:

Summary: To subtract two or more fractions that have the same denominators, subtract the numerators and place the resulting difference over the common denominator. Simplify your result, if necessary.

Exercises

Directions: Subtract the fractions in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.

Note: To write the fraction three-fourths, enter 3/4 into the form. To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.

1.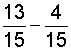
	ANSWER BOX:    RESULTS BOX:

2.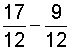
	ANSWER BOX:    RESULTS BOX:

3.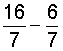
	ANSWER BOX:    RESULTS BOX:

4.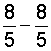
	ANSWER BOX:    RESULTS BOX:

5.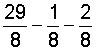
	ANSWER BOX:    RESULTS BOX: