Learn How to Solve Fraction Word Problems with Examples and Interactive Exercises
Example 1: Rachel rode her bike for one-fifth of a mile on Monday and two-fifths of a mile on Tuesday. How many miles did she ride altogether?
Analysis: To solve this problem, we will add two fractions with like denominators.
Solution:
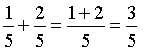
Answer: Rachel rode her bike for three-fifths of a mile altogether.
Example 2: Stefanie swam four-fifths of a lap in the morning and seven-fifteenths of a lap in the evening. How much farther did Stefanie swim in the morning than in the evening?
Analysis: To solve this problem, we will subtract two fractions with unlike denominators.
Solution:
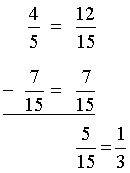
Answer: Stefanie swam one-third of a lap farther in the morning.
Example 3: It took Nick five-thirds of an hour to complete his math homework on Monday, three-fourths of an hour on Tuesday, and five-sixths of an hour on Wednesday. How many hours did he take to complete his homework altogether?
Analysis: To solve this problem, we will add three fractions with unlike denominators. Note that the first is an improper fraction.
Solution:
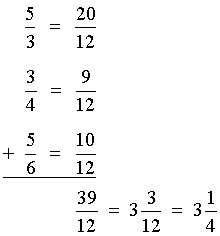
Answer: It took Nick three and one-fourth hours to complete his homework altogether.
Example 4: Dina added five-sixths of a bag of soil to her garden. Her neighbor Natasha added eleven-eighths bags of soil to her garden. How much more soil did Natasha add than Dina?
Analysis: To solve this problem, we will subtract two fractions with unlike denominators.
Solution:
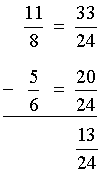
Answer:
Example 5: At a pizza party, Diego and his friends ate three and one-fourth cheese pizzas and two and three-fourths pepperoni pizzas. How much pizza did they eat in all?
Analysis: To solve this problem, we will add two mixed numbers, with the fractional parts having like denominators.
Solution:
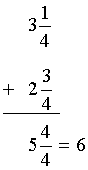
Answer: Diego and his friends ate six pizzas in all.
Example 6: The Cocozzelli family drove their car for five and five-sixths days to reach their vacation home, and then drove for six and one-sixth days to return home. How much longer did it take them to drive home?
Analysis: To solve this problem, we will subtract two mixed numbers, with the fractional parts having like denominators.
Solution:
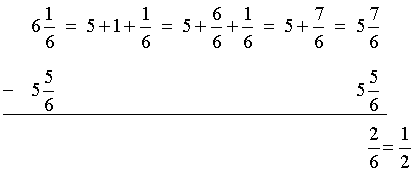
Answer: The Cocozzelli family took one-half more days to drive home.
Example 7: A warehouse has 12 and nine-tenths meters of tape in one area of the building, and eight and three-fifths meters of tape in another part. How much tape does the warehouse have in all?
Analysis: To solve this problem, we will add two mixed numbers, with the fractional parts having unlike denominators.
Solution:
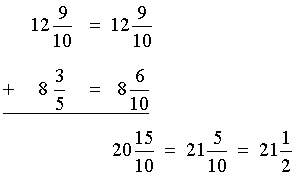
Answer: The warehouse has 21 and one-half meters of tape in all.
Example 8: An electrician has three and seven-sixteenths cm of wire. He needs only two and five-eighths cm of wire for a job. How much wire does he need to cut?
Analysis: To solve this problem, we will subtract two mixed numbers, with the fractional parts having unlike denominators.
Solution:
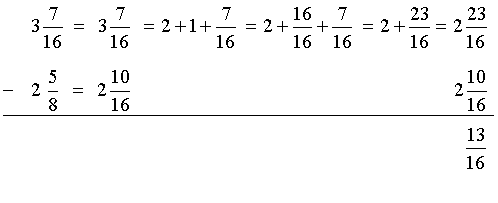
Answer: The electrician needs to cut 13 sixteenths cm of wire.
Example 9: A carpenter had a piece of wood that was 15 feet in length. If he needs only 10 and five-twelfths feet of wood, then how much wood should he cut?
Analysis: To solve this problem, we will subtract a mixed number from a whole number.
Solution:
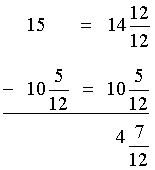
Answer: The carpenter needs to cut four and seven-twelfths feet of wood.
Summary: In this lesson we learned how to solve word problems involving addition and subtraction of fractions and mixed numbers. We used the following skills to solve these problems:
- Add fractions with like denominators.
- Subtract fractions with like denominators.
- Find the LCD.
- Add fractions with unlike denominators.
- Subtract fractions with unlike denominators.
- Add mixed numbers with like denominators.
- Subtract mixed numbers with like denominators.
- Add mixed numbers with unlike denominators.
- Subtract mixed numbers with unlike denominators.
Exercises
Directions: Subtract the mixed numbers in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
Note: To write the fraction three-fourths, enter 3/4 into the form. To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.
| 1. | A recipe needs 3/4 teaspoon black pepper and 1/4 red pepper. How much more black pepper is needed than red pepper for this recipe? |
| 2. | One evening, a restaurant served a total of 1/2 of a loaf of wheat bread and 7/8 of a loaf of white bread. How many loaves were served in all? |
| 3. | Robin and Kelly own neighboring cornfields. Robin harvested 4 and 3/10 acres of corn on Monday and Kelly harvested 2 and 1/10 acres. How many more acres did Robin harvest than Kelly? |
| 4. | Juanita needed 3 and 2/3 hours to take a standardized test, and Jordan needed 5 and 1/4 hours. How much more time did Jordan need than Juanita to take the test? |
| 5. | An airline agent checked in 10 and 1/3 kg of baggage for one passenger and another 8 and 5/6 kg of baggage for his travel companion. How many kilograms of luggage did the agent check in all? |
