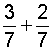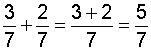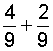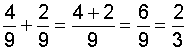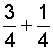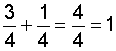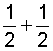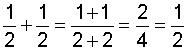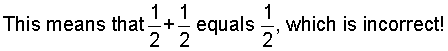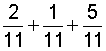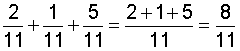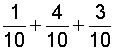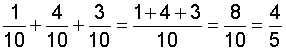To add or subtract items, the units must be the same. For example, look at the items being added below.
2 apples + 3 apples = 5 apples
6 oranges + 3 oranges = 9 oranges
2 quarters + 5 quarters = 7 quarters
2 nickels + 3 nickels = 5 nickels
We cannot add apples and oranges unless we call them "fruits". Similarly, we cannot add quarters and nickels unless we call them "cents". In the name of a fraction, the unit is the denominator. For example, in the fraction "4 tenths", the unit is the denominator, tenths. Therefore, 4 tenths + 5 tenths = 9 tenths. Look at example 1 below.
 Example 1: A pizza was divided into eight equal parts (slices). If Jenny ate five slices and Eric ate two slices, then what part of the pizza did they eat altogether?
Example 1: A pizza was divided into eight equal parts (slices). If Jenny ate five slices and Eric ate two slices, then what part of the pizza did they eat altogether?
Analysis: Jenny ate "5 eighths" of the pizza and Eric ate "2 eighths". In each of these fractions, the unit is the denominator, eighths. Since both fractions have the same units, we can add them together.
Solution: "5 eighths + 2 eighths = 7 eighths."
The denominator of a fraction names what we are counting. In example 1, we are counting eighths. This is illustrated on the number line below.
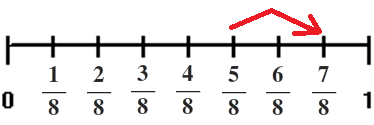
It is not always practical to draw a number line. So we need an arithmetic procedure for adding fractions. The problem from example 1 is written using mathematical notation below:
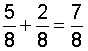
The denominator of a fraction names the unit. The numerator indicates how many there are. For example, in the fraction five-eighths, the unit is eighths and there are 5 of them. In order to add fractions, the denominators must be the same. That is, they must have a common denominator.
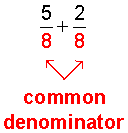
These fractions have a common denominator (the denominators are the same). If the denominators were not common, you could not add these fractions.
This leads us to the following procedure for adding fractions with a common denominator.
Procedure: To add two or more fractions that have the same denominators, add the numerators and place the resulting sum over the common denominator. Simplify your result, if necessary.
Let's look at some examples of adding fractions using this procedure.
|
|
In example 3, we needed to simplify the result: We reduced six-ninths to lowest terms, which is two-thirds.
|
In example 4, we simplified the result by converting the improper fraction to a whole number.
Avoid This Common Mistake!
Some students mistakenly add the denominators as well as the numerators. This is mathematically incorrect, as shown below.
|
Do not add denominators!
To add fractions, add only the numerators, and place the sum over the common denominator.
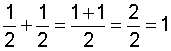
So far, we have added only two fractions at a time. We can add more than two fractions using the procedure above. This is shown in the examples below.
|
|
Summary:
To add two or more fractions that have the same denominators, add the numerators and place the resulting sum over the common denominator. Simplify your result, if necessary.
Exercises
Directions: Add the fractions in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
Note: To write the fraction three-fourths, enter 3/4 into the form.
| 1. | 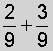 |
| 2. | 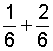 |
| 3. | 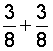 |
| 4. | 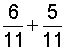 |
| 5. | 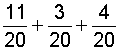 |