
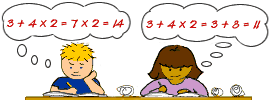 Problem: Evaluate the following arithmetic expression:
Problem: Evaluate the following arithmetic expression:
3 + 4 x 2
Solution:
| Student 1 | Student 2 | |||
| 3 + 4 x 2 | 3 + 4 x 2 | |||
| = 7 x 2 | = 3 + 8 | |||
| = 14 | = 11 |
It seems that each student interpreted the problem differently, resulting in two different answers. Student 1 performed the operation of addition first, then multiplication; whereas student 2 performed multiplication first, then addition. When performing arithmetic operations there can be only one correct answer. We need a set of rules in order to avoid this kind of confusion. Mathematicians have devised a standard order of operations for calculations involving more than one arithmetic operation.
Rule 1: First perform any calculations inside parentheses.
Rule 2: Next perform all multiplications and divisions, working from left to right.
Rule 3: Lastly, perform all additions and subtractions, working from left to right.
An easy way to remember this order is to use the acronym PEMDAS (parentheses, exponents, multiplication and division, addition and subtraction).
The above problem was solved correctly by Student 2, since she followed Rules 2 and 3. Let's look at some examples of solving arithmetic expressions using these rules.
Example 1: Evaluate each expression using the rules for PEMDAS.
Solution:
| Order of Operations | ||
| Expression | Evaluation | Operation |
| 6 + 7 x 8 | = 6 + 7 x 8 | Multiplication |
| = 6 + 56 | Addition | |
| = 62 | ||
| 16 ÷ 8 - 2 | = 16 ÷ 8 - 2 | Division |
| = 2 - 2 | Subtraction | |
| = 0 | ||
| (25 - 11) x 3 | = (25 - 11) x 3 | Parentheses |
| = 14 x 3 | Multiplication | |
| = 42 | ||
In Example 1, each problem involved only 2 operations. Let's look at some examples that involve more than two operations.
Example 2: Evaluate 3 + 6 x (5 + 4) ÷ 3 - 7 using PEMDAS.
Solution:
| Step 1: | 3 + 6 x (5 + 4) ÷ 3 - 7 | = | 3 + 6 x 9 ÷ 3 - 7 | Parentheses |
| Step 2: | 3 + 6 x 9 ÷ 3 - 7 | = | 3 + 54 ÷ 3 - 7 | Multiplication |
| Step 3: | 3 + 54 ÷ 3 - 7 | = | 3 + 18 - 7 | Division |
| Step 4: | 3 + 18 - 7 | = | 21 - 7 | Addition |
| Step 5: | 21 - 7 | = | 14 | Subtraction |
Example 3: Evaluate 9 - 5 ÷ (8 - 3) x 2 + 6 using PEMDAS.
Solution:
| Step 1: | 9 - 5 ÷ (8 - 3) x 2 + 6 | = | 9 - 5 ÷ 5 x 2 + 6 | Parentheses |
| Step 2: | 9 - 5 ÷ 5 x 2 + 6 | = | 9 - 1 x 2 + 6 | Division |
| Step 3: | 9 - 1 x 2 + 6 | = | 9 - 2 + 6 | Multiplication |
| Step 4: | 9 - 2 + 6 | = | 7 + 6 | Subtraction |
| Step 5: | 7 + 6 | = | 13 | Addition |
In Examples 2 and 3, you will notice that multiplication and division were evaluated from left to right according to Rule 2. Similarly, addition and subtraction were evaluated from left to right, according to Rule 3.
When two or more operations occur inside a set of parentheses, these operations should be evaluated according to Rules 2 and 3. This is done in Example 4 below.
Example 4: Evaluate 150 ÷ (6 + 3 x 8) - 5 using the PEMDAS.
Solution:
| Step 1: | 150 ÷ (6 + 3 x 8) - 5 | = | 150 ÷ (6 + 24) - 5 | Multiplication inside Parentheses |
| Step 2: | 150 ÷ (6 + 24) - 5 | = | 150 ÷ 30 - 5 | Addition inside Parentheses |
| Step 3: | 150 ÷ 30 - 5 | = | 5 - 5 | Division |
| Step 4: | 5 - 5 | = | 0 | Subtraction |
Example 5: Evaluate the arithmetic expression below:
![]()
Solution: This problem includes a fraction bar (also called a vinculum), which means we must divide the numerator by the denominator. However, we must first perform all calculations above and below the fraction bar BEFORE dividing.
Thus![]()
Evaluating this expression, we get:
![]()
Example 6: Write an arithmetic expression for this problem. Then evaluate the expression using PEMDAS.
Mr. Smith charged Jill $32 for parts and $15 per hour for labor to repair her bicycle. If he spent 3 hours repairing her bike, how much does Jill owe him?
Solution: 32 + 3 x 15 = 32 + 3 x 15 = 32 + 45 = 77
Jill owes Mr. Smith $77.
Summary: When evaluating arithmetic expressions, the operation order is:
- Simplify all operations inside parentheses.
- Perform all multiplications and divisions, working from left to right.
- Perform all additions and subtractions, working from left to right.
If a problem includes a fraction bar, perform all calculations above and below the fraction bar before dividing the numerator by the denominator.
Exercises
Directions: Complete each exercise by applying the rules for order of operations. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. |
9 + 6 x (8 - 5) |
| 2. |
(14 - 5) ÷ (9 - 6) |
| 3. |
5 x 8 + 6 ÷ 6 - 12 x 2 |
| 4. |
| 5. |
A caterer charges a setup fee of $50, plus $20 per person. How much will the caterer charge if 35 people attend the party, and the customer has a coupon for $100 off the total? |




