|
|
| Addition Rules
for Probability |
 |
Unit 6 > Lesson 6 of 12 |
| Experiment 1: |
A single 6-sided die is rolled. What is the probability of rolling a 2 or a 5? |
 
|
| Possibilities: |
| 1. |
The number rolled can be a 2. |
| 2. |
The number rolled can be a 5. |
|
| Events: |
These events are mutually exclusive since they cannot occur at the same time. |
| Probabilities: |
How do we find the probabilities of these mutually exclusive events? We need a rule to
guide us.
|
| Addition Rule 1: |
When two events, A and B, are mutually exclusive, the probability that A or B will occur
is the sum of the probability of each event. |
| |
P(A or B) = P(A) + P(B) |
Let's use this addition rule to find the probability for Experiment 1.
| Experiment 1: |
A single 6-sided die is rolled. What is the probability of rolling a 2 or a 5? |
|
| Probabilities: |
| P(2) |
= |
1 |
| 6 |
|
|
| P(5) |
= |
1 |
| 6 |
|
|
| P(2 or 5) |
= |
P(2) |
+ |
P(5) |
|
|
| |
= |
1 |
+ |
1 |
| 6 |
6 |
|
|
| = |
2 |
| 6 |
|
|
| = |
1 |
| 3 |
|
| Experiment 2: |
A spinner has 4 equal sectors colored yellow, blue, green, and red. What is the
probability of landing on red or blue after spinning this spinner?
|
|
|
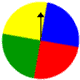
| Probabilities: |
| P(red) |
= |
1 |
| 4 |
|
|
| P(blue) |
= |
1 |
| 4 |
|
|
| P(red or blue) |
= |
P(red) |
+ |
P(blue) |
|
|
| |
= |
1 |
+ |
1 |
| 4 |
4 |
|
|
| = |
2 |
| 4 |
|
|
| = |
1 |
| 2 |
|
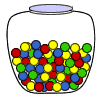| Experiment 3: |
A glass jar contains 1 red, 3 green, 2 blue, and 4 yellow marbles. If a
single marble is chosen at random from the jar, what is the probability that it is yellow or green?
|
|
![[IMAGE]](images/marbles_jar.gif)
|
| Probabilities: |
| P(yellow) |
= |
4 |
| 10 |
|
|
| P(green) |
= |
3 |
| 10 |
|
|
| P(yellow or green) |
= |
P(yellow) |
+ |
P(green) |
|
|
| |
= |
4 |
+ |
3 |
| 10 |
10 |
|
|
| = |
7 |
| 10 |
|
|
In each of the three experiments above, the events are mutually exclusive. Let's look
at some experiments in which the events are non-mutually exclusive. |
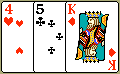| Experiment 4: |
A single card is chosen at random from a standard deck of 52 playing
cards. What is the probability of choosing a king or a club?
|
|
![[IMAGE]](images/poker_hand.gif)
|
| Probabilities: |
| P(king or club) |
= |
P(king) |
+ |
P(club) |
- |
P(king of clubs) |
|
|
| |
= |
4 |
+ |
13 |
- |
1 |
| 52 |
52 |
52 |
|
|
| = |
16 |
| 52 |
|
|
| = |
4 |
| 13 |
|
|
In Experiment 4, the events are non-mutually exclusive. The addition causes the king of
clubs to be counted twice, so its probability must be subtracted. When two events are non-mutually exclusive, a
different addition rule must be used. | |
| Addition Rule 2: |
When two events, A and B, are non-mutually exclusive, the
probability that A or B will occur is:
|
| |
P(A or B) = P(A) + P(B) - P(A and B) |
| In the rule above, P(A and B) refers to the overlap of the two events. Let's
apply this rule to some other experiments. | |
| Experiment 5: |
In a math class of 30 students, 17 are boys and 13 are girls. On a unit test,
4 boys and 5 girls made an A grade. If a student is chosen at random from the class, what is the
probability of choosing a girl or an A student?
|
![[IMAGE]](images/Agrade_girl.gif)
|
| Probabilities: |
| P(girl or A) |
= |
P(girl) |
+ |
P(A) |
- |
P(girl and A) |
|
|
| |
= |
13 |
+ |
9 |
- |
5 |
| 30 |
30 |
30 |
|
|
| = |
17 |
| 30 |
|
| Experiment 6: |
On New Year's Eve, the probability of a person having a car accident is 0.09. The probability of a person driving while intoxicated is 0.32 and probability of a person having a car accident while intoxicated is 0.15. What is the probability of a person driving while intoxicated or having a car accident?
|
![[IMAGE]](images/car_crash.gif)
|
| Probabilities: |
| P(intoxicated or accident) |
= |
P(intoxicated) |
+ |
P(accident) |
- |
P(intoxicated and accident) |
|
|
| |
= |
0.32 |
+ |
0.09 |
- |
0.15 |
| |
= |
0.26 |
|
|
| Summary: |
To find the probability of event A or B, we must first determine whether the events are
mutually exclusive or non-mutually exclusive. Then we can apply the appropriate Addition
Rule:
|
| |
| Addition Rule 1: |
When two events, A and B, are mutually exclusive, the
probability that A or B will occur is the sum of the probability of each event.
|
|
P(A or B) = P(A) + P(B) |
| |
| Addition Rule 2:: |
When two events, A and B, are non-mutually exclusive, there is some
overlap between these events. The probability that A or B
will occur is the sum of the probability of each event, minus the probability of the
overlap. |
|
P(A or B) = P(A) + P(B) - P(A and B) |
|
Exercises
| Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer
is provided in the RESULTS BOX. If you make a mistake, choose a different button. |
| 1. |
A day of the week is chosen at random. What is the probability of choosing a Monday or Tuesday?
|
| | |
| |
|
| 2. |
In a pet store, there are 6 puppies, 9 kittens, 4 gerbils and 7 parakeets. If a pet is chosen at random,
what is the probability of choosing a puppy or a parakeet?
|
| | |
| |
|
| 3. |
The probability of a New York teenager owning a skateboard is 0.37, of owning a bicycle is 0.81 and of owning both is 0.36. If a New York teenager is chosen at random, what is the
probability that the teenager owns a skateboard or a bicycle? |
| | |
| |
|
| 4. |
A number from 1 to 10 is chosen at random. What is the probability of choosing a
5 or an even number? |
| | |
| |
|
| 5. |
A single 6-sided die is rolled. What is the probability of rolling a number greater than 3 or an even
number?
|
| | |
| |
|
Unit 6: Probability Theory
|
Interactive Math Goodies Software
