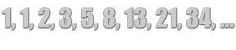
 Problem 1: The area of a rectangular garden is 7 square yards. List all possible whole-number dimensions the garden can have.
Problem 1: The area of a rectangular garden is 7 square yards. List all possible whole-number dimensions the garden can have.
Solution: 1 yd x 7 yd
The whole-number dimensions, 1 and 7, of the rectangular garden above, are the factors of the number 7.
Problem 2: The area of a rectangular garden is 8 square yards. List all possible whole-number dimensions the garden can have.
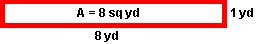
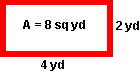
Solution: 1 yd x 8 yd, 2 yd x 4 yd
The whole-number dimensions, 1, 2, 4 and 8, of the rectangular gardens in Problem 2, are the factors of the number 8. In Problem 1, the number 7 has only two factors. The number 7 is prime. In problem 2 above, the number 8 has four factors. The number 8 is composite.
Definitions
- A prime number has only two factors: 1 and itself.
- A composite number has more than two factors.
- The number 1 is neither prime nor composite.
When the area of a rectangle is a prime number, there is only one set of possible dimensions for that rectangle. When the area of a rectangle is a composite number, there are two or more sets of possible dimensions for that rectangle. Each set of dimensions is a pair of factors.
To determine if a number is prime or composite, follow these steps:
- Find all factors of the number.
- If the number has only two factors, 1 and itself, then it is prime.
- If the number has more than two factors, then it is composite.
Example 1: Is the number 2 prime or composite?
Solution: The factors of 2 are 1 x 2. 2 is prime.
Example 2: Is the number 9 prime or composite?
Solution: The factors of 9 are 1 x 9, 3 x 3. 9 is composite.
We have determined if a single number is prime or composite. Let's look at a range of numbers to see if they are prime or composite. Please note that each range of numbers given in Examples 3, 4 and 5 below are inclusive.
Example 3: Find all prime numbers between 2 and 9.
| factors of 2: | 1 x 2 | 2 is prime |
| factors of 3: | 1 x 3 | 3 is prime |
| factors of 4: | 1 x 4, 2 x 2 | 4 is composite |
| factors of 5: | 1 x 5 | 5 is prime |
| factors of 6: | 1 x 6, 2 x 3 | 6 is composite |
| factors of 7: | 1 x 7 | 7 is prime |
| factors of 8: | 1 x 8, 2 x 4 | 8 is composite |
| factors of 9: | 1 x 9, 3 x 3 | 9 is composite |
Solution: The prime numbers between 2 and 9 are 2, 3, 5 and 7. 
Example 4: Find all prime numbers between 10 and 19.
| factors of 10: | 1 x 10, 2 x 5 | 10 is composite |
| factors of 11: | 1 x 11 | 11 is prime |
| factors of 12: | 1 x 12, 2 x 6, 3 x 4 | 12 is composite |
| factors of 13: | 1 x 13 | 13 is prime |
| factors of 14: | 1 x 14, 2 x 7 | 14 is composite |
| factors of 15: | 1 x 15, 3 x 5 | 15 is composite |
| factors of 16 | 1 x 16, 4 x 4 | 16 is composite |
| factors of 17: | 1 x 17 | 17 is prime |
| factors of 18: | 1 x 18, 3 x 6 | 18 is composite |
| factors of 19: | 1 x 19 | 19 is prime |
Solution: The prime numbers between 10 and 19 are 11, 13, 17 and 19. 
Example 5: Find all prime numbers between 20 and 29.
| factors of 20: | 1 x 20, 2 x 10, 4 x 5 | 20 is composite |
| factors of 21: | 1 x 21, 3 x 7 | 21 is composite |
| factors of 22: | 1 x 22, 2 x 11 | 22 is composite |
| factors of 23: | 1 x 23 | 23 is prime |
| factors of 24: | 1 x 24, 2 x 12, 3 x 8, 4 x 6 | 24 is composite |
| factors of 25: | 1 x 25, 5 x 5 | 25 is composite |
| factors of 26: | 1 x 26, 2 x 13 | 26 is composite |
| factors of 27: | 1 x 27, 3 x 9 | 27 is composite |
| factors of 28: | 1 x 28, 2 x 14, 4 x 7 | 28 is composite |
| factors of 29: | 1 x 29 | 29 is prime |
Solution: The prime numbers between 20 and 29 are 23 and 29. 
 Example 6: Is the number 31 prime or composite? Explain your answer using full sentences.
Example 6: Is the number 31 prime or composite? Explain your answer using full sentences.
Solution 1: The number 31 is prime because its only factors are one and itself.
Solution 2: Thirty-one is a prime number. This is because the number 31 has only two factors: 1 and 31.
Solution 3: I divided the number 31 by all numbers between 1 and 31 and found no factors other than one and thirty-one. Therefore, 31 is prime.
There are many possible ways to explain the solution to this problem. These are just three possible explanations.
Summary: A prime number has only two factors: 1 and itself. A composite number has more than two factors. The number 1 is neither prime nor composite.
The prime numbers between 2 and 31 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and 31 since each of these numbers has only two factors, itself and 1.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. | Each of the following numbers is composite EXCEPT: 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 |
| 2. | The prime numbers between 40 and 49 are: |
| 3. | The prime numbers between 50 and 59 are: |
| 4. | The prime numbers between 60 and 69 are: |
| 5. | The prime numbers between 20 and 69 are: |




