A circle is a shape with all points the same distance from the center. It is named by the center. The circle to the left is called circle A since the center is at point A. If you measure the distance around a circle and divide it by the distance across the circle through the center, you will always come close to a particular value, depending upon the accuracy of your measurement. This value is approximately 3.14159265358979323846... We use the Greek letter
A circle is a shape with all points the same distance from the center. It is named by the center. The circle to the left is called circle A since the center is at point A. If you measure the distance around a circle and divide it by the distance across the circle through the center, you will always come close to a particular value, depending upon the accuracy of your measurement. This value is approximately 3.14159265358979323846... We use the Greek letter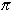 (pronounced Pi) to represent this value. The number
(pronounced Pi) to represent this value. The number 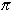 goes on forever. However, using computers,
goes on forever. However, using computers, 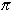 has been calculated to over 1 trillion digits past the decimal point.
has been calculated to over 1 trillion digits past the decimal point.
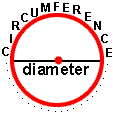 The distance around a circle is called the circumference. The distance across a circle through the center is called the diameter.
The distance around a circle is called the circumference. The distance across a circle through the center is called the diameter. 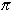 is the ratio of the circumference of a circle to the diameter. Thus, for any circle, if you divide the circumference by the diameter, you get a value close to
is the ratio of the circumference of a circle to the diameter. Thus, for any circle, if you divide the circumference by the diameter, you get a value close to 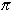 . This relationship is expressed in the following formula:
. This relationship is expressed in the following formula:
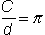
where 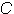 is circumference and
is circumference and 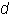 is diameter. You can test this formula at home with a round dinner plate. If you measure the circumference and the diameter of the plate and then divide
is diameter. You can test this formula at home with a round dinner plate. If you measure the circumference and the diameter of the plate and then divide 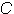 by
by 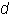 , your quotient should come close to
, your quotient should come close to 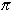 . Another way to write this formula is:
. Another way to write this formula is: 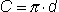 where · means multiply. This second formula for finding the circumference is commonly used in problems where the diameter is given and the circumference is not known (see the examples below).
where · means multiply. This second formula for finding the circumference is commonly used in problems where the diameter is given and the circumference is not known (see the examples below).
 The radius of a circle is the distance from the center of a circle to any point on the circle. If you place two radii end-to-end in a circle, you would have the same length as one diameter. Thus, the diameter of a circle is twice as long as the radius. This relationship is expressed in the following circumference of a circle formula:
The radius of a circle is the distance from the center of a circle to any point on the circle. If you place two radii end-to-end in a circle, you would have the same length as one diameter. Thus, the diameter of a circle is twice as long as the radius. This relationship is expressed in the following circumference of a circle formula: 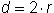 , where
, where 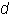 is the diameter and
is the diameter and 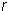 is the radius.
is the radius.
 Circumference, diameter and radii are measured in linear units, such as inches and centimeters. A circle has many different radii and many different diameters, each passing through the center. A real-life example of a radius is the spoke of a bicycle wheel. A 9-inch pizza is an example of a diameter: when one makes the first cut to slice a round pizza pie in half, this cut is the diameter of the pizza. So a 9-inch pizza has a 9-inch diameter. Let's look at some examples of finding the circumference. In these examples, we will use
Circumference, diameter and radii are measured in linear units, such as inches and centimeters. A circle has many different radii and many different diameters, each passing through the center. A real-life example of a radius is the spoke of a bicycle wheel. A 9-inch pizza is an example of a diameter: when one makes the first cut to slice a round pizza pie in half, this cut is the diameter of the pizza. So a 9-inch pizza has a 9-inch diameter. Let's look at some examples of finding the circumference. In these examples, we will use 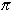 = 3.14 to simplify our calculations.
= 3.14 to simplify our calculations.
Example 1: The radius of a circle is 2 inches. What is the diameter?
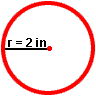 Solution:
Solution:
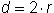
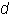 = 2 · (2 in)
= 2 · (2 in)
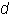 = 4 in
= 4 in
Example 2: The diameter of a circle is 3 centimeters. What is the circumference?
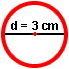 Solution:
Solution:
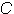 =
= 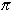 *
* 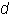
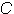 = 3.14 · (3 cm)
= 3.14 · (3 cm)
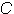 = 9.42 cm
= 9.42 cm
Example 3: The radius of a circle is 2 inches. What is the circumference?
 Solution:
Solution:
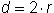
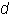 = 2 · (2 in)
= 2 · (2 in)
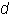 = 4 in
= 4 in
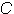 =
= 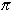 *
* 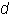
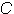 = 3.14 · (4 in)
= 3.14 · (4 in)
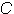 = 12.56 in
= 12.56 in
Example 4: The circumference of a circle is 15.7 centimeters. What is the diameter?
 Solution:
Solution:
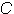 =
= 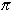 *
* 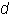
15.7 cm = 3.14 · 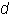
15.7 cm ÷ 3.14 = 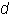
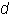 = 15.7 cm ÷ 3.14
= 15.7 cm ÷ 3.14
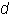 = 5 cm
= 5 cm
Summary: The number 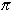 is the ratio of the circumference of a circle to its diameter. The value of
is the ratio of the circumference of a circle to its diameter. The value of 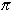 is approximately 3.14159265358979323846...The diameter of a circle is twice the radius. Given the diameter or radius of a circle, we can find the circumference. We can also find the diameter (and radius) of a circle given the circumference. The formulas for diameter and circumference are listed below. We round
is approximately 3.14159265358979323846...The diameter of a circle is twice the radius. Given the diameter or radius of a circle, we can find the circumference. We can also find the diameter (and radius) of a circle given the circumference. The formulas for diameter and circumference are listed below. We round 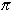 to 3.14 in order to simplify our calculations.
to 3.14 in order to simplify our calculations.
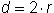
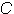 =
= 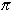 *
* 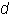
For additional help, watch the Circumference of a Circle video
Exercises
Circumference of a circle questions: Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR. Use 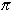 = 3.14 to calculate your answers.
= 3.14 to calculate your answers.
| 1. | The diameter of a nickel is 2 centimeters. What is the circumference? |
| 2. | The circumference of a bicycle wheel is 50.24 inches. What is the diameter? |
| 3. | The radius of a circular rug is 4 feet. What is the circumference? |
| 4. | The circumference of a compact disc is 28.26 centimeters. What is the radius? |
| 5. | The diameter of your bicycle wheel is 25 inches. How far will you move in one turn of your wheel? |