Learn About Area of a Triangle With The Following Examples And Interactive Exercises
 The area of a polygon is the number of square units inside that polygon. Area is 2-dimensional like a carpet or an area rug. A triangle is a three-sided polygon. We will look at several types of triangles in this lesson.
The area of a polygon is the number of square units inside that polygon. Area is 2-dimensional like a carpet or an area rug. A triangle is a three-sided polygon. We will look at several types of triangles in this lesson.
 To find the area of a triangle, multiply the base by the height, and then divide by 2. The division by 2 comes from the fact that a parallelogram can be divided into 2 triangles. For example, in the diagram to the left, the area of each triangle is equal to one-half the area of the parallelogram.
To find the area of a triangle, multiply the base by the height, and then divide by 2. The division by 2 comes from the fact that a parallelogram can be divided into 2 triangles. For example, in the diagram to the left, the area of each triangle is equal to one-half the area of the parallelogram.
Since the area of a parallelogram is A = B * H, the area of a triangle must be one-half the area of a parallelogram. Thus, the formula for the area of a triangle is:
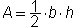 or
or 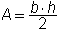
where b is the base, h is the height and · means multiply.
The base and height of a triangle must be perpendicular to each other. In each of the examples below, the base is a side of the triangle. However, depending on the triangle, the height may or may not be a side of the triangle. For example, in the right triangle in Example 2, the height is a side of the triangle since it is perpendicular to the base. In the triangles in Examples 1 and 3, the lateral sides are not perpendicular to the base, so a dotted line is drawn to represent the height.
Example 1: Find the area of an acute triangle with a base of 15 inches and a height of 4 inches.
Solution:
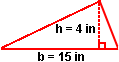
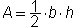
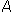 =
= 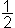 · (15 in) · (4 in)
· (15 in) · (4 in)
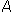 =
= 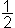 · (60 in2)
· (60 in2)
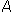 = 30 in2
= 30 in2
Example 2: Find the area of a right triangle with a base of 6 centimeters and a height of 9 centimeters.
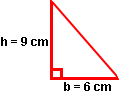 Solution:
Solution:
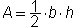
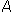 =
= 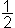 · (6 cm) · (9 cm)
· (6 cm) · (9 cm)
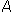 =
= 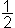 · (54 cm2)
· (54 cm2)
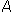 = 27 cm2
= 27 cm2
Example 3: Find the area of an obtuse triangle with a base of 5 inches and a height of 8 inches.
Solution:
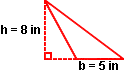
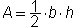
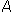 =
= 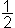 · (5 in) · (8 in)
· (5 in) · (8 in)
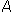 =
= 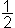 · (40 in2)
· (40 in2)
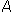 = 20 in2
= 20 in2
Example 4: A triangle shaped mat has an area of 18 square feet and the base is 3 feet. Find the height. (Note: The triangle in the illustration to the right is NOT drawn to scale.)
Solution:
In this example, we are given the area of a triangle and one dimension, and we are asked to work backwards to find the other dimension.
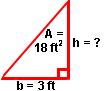
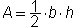
18 ft2 = 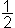 \B7 (3 ft) · h
\B7 (3 ft) · h
Multiplying both sides of the equation by 2, we get:
36 ft2 = (3 ft) · h
Dividing both sides of the equation by 3 ft, we get:
12 ft = h
Commuting this equation, we get:
h = 12 ft
Summary: Given the base and the height of a triangle, we can find the area. Given the area and either the base or the height of a triangle, we can find the other dimension. The formula for area of a triangle is:
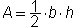 or
or 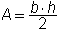 where b is the base and h is the height.
where b is the base and h is the height.
Exercises
Directions: Read each question below. Click once in an ANSWER BOX and type in your answer; then click ENTER. Your answers should be given as whole numbers greater than zero. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. | Find the area of a triangle with a base of 16 feet and a height of 3 feet. |
| 2. | Find the area of a triangle with a base of 4 meters and a height of 14 meters. |
| 3. | Find the area of a triangle with a base of 18 inches and a height of 2 inches. |
| 4. | A triangle shaped piece of paper has an area of 36 square centimeters and a base of 6 centimeters. Find the height. (Hint: work backwards) |
| 5. | A triangle shaped rug has an area of 12 square yards and the height is 3 yards. Find the base. (Hint: work backwards) |




