Problem 1: Do you see a pattern in each table below? (Mouse over the red text)
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
 In Table 1, we are multiplying the decimal 0.2658 by powers of 10. Each time we multiply by a power of 10, the decimal point is moved one place to the right. In Table 2, we are dividing the whole number 265,800. by powers of 10. Each time we divide by a power of 10, the decimal point is moved one place to the left. These patterns occur because a decimal is any number in our base-ten number system, and decimal places change by a factor of 10.
In Table 1, we are multiplying the decimal 0.2658 by powers of 10. Each time we multiply by a power of 10, the decimal point is moved one place to the right. In Table 2, we are dividing the whole number 265,800. by powers of 10. Each time we divide by a power of 10, the decimal point is moved one place to the left. These patterns occur because a decimal is any number in our base-ten number system, and decimal places change by a factor of 10.
Problem 2: Which is greater: 56.5 x 80 or 8 x 565? Explain your answer.
Analysis: 56.5 x 80 = 56.5 x (10 x 8) = (56.5 x 10) x 8 = 565 x 8
Answer: They are equal.
As you can see in the problem above, multiplying one factor by a power of 10 and dividing the other factor by the same power of 10 maintains the equality of the expression. Thus, since 56.5 x 10 = 565, and since 80 ÷ 10 = 8, the expressions 56.5 x 80 and 8 x 565 are equal. Now that we have seen these patterns, we can look at some more problems.
 Example 1: An electrician earns $18.75 per hour. If he worked 200 hours this month, then how much did he earn?
Example 1: An electrician earns $18.75 per hour. If he worked 200 hours this month, then how much did he earn?
Analysis: The electrician earns $18.75 for each hour worked. For 200 hours of work, he will earn $18.75, a total of 200 times. We can multiply to solve this problem.
Step 1: Estimate the product.
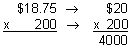
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
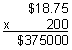
Compensate by placing the decimal point in the product.
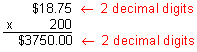
Step 3: Compare the estimate with the product to verify that your answer makes sense.
Our product of $3,750.00 makes sense since it is close to our estimate of $4,000.00
Answer: The electrician earned $3,750.00 for 200 hours of work.
When multiplying a decimal by a whole number, placement of the decimal point is very important. Since there are two decimal digits in the factor $18.75, there must be two decimal digits in the product $3,750.00. This is because hundredths x whole number = hundredths. Estimating the product lets us verify that the placement of the decimal point is correct, and that we have a reasonable answer. For example, if our estimate was $4,000.00 and our product was $375.00, then we would know that we made a multiplication error. Let's look at some more examples of multiplying a decimal by a whole number.
Example 2: Multiply: 22.6 x 38
Analysis: There is one decimal digit in the factor 22.6. The whole number 38 is not a multiple of 10.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
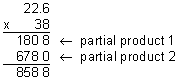
Compensate by placing the decimal point in the product.
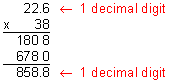
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 858.8 makes sense since it is close to our estimate of 800.
Answer: The product of 22.6 and 38 is 858.8.
In Example1, the whole number 200 is a multiple of 10. However, In Example 2, the whole number 38 is not a multiple of 10, which led to partial products when we multiplied. Since there is one decimal digit in the factor 22.6, there must be one decimal digit in the product. Perhaps you are wondering why this is so. When we ignored the decimal point in Step 2, we really moved it one place to the right (22.6 x 10 = 226.). Since we multiplied 22.6 by a power of 10, we need to compensate to get the right answer. To do this, we must divide by that power of 10 when we place the decimal point in our answer: Start from the right of the last digit in the product, and move the decimal point one place to the left. Let's look at another example.
Example 3: Multiply: 427 x 0.037
Analysis: There are three decimal digits in the factor 0.037.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
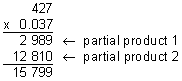
Compensate by placing the decimal point in the product.

Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 15.799 makes sense since it is close to our estimate of 16.
Answer: The product of 427 and 0.037 is 15.799.
Look at the example above. Since there are three decimal digits in the factor 0.037, there must be three decimal digits in the product. When we ignored the decimal point in Step 2, we really moved it three places to the right (0.037 x 1,000 = 37.) Since we multiplied 0.037 by a power of 10, we need to compensate to get the right answer. To do this, we must divide by that power when we place the decimal point in our answer: Start from the right of the last digit in the product, and move the decimal point three places to the left. Let's look at another example.
Example 4: Multiply: 0.874 x 401
Analysis: There are three decimal digits in the factor 0.874.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
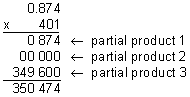
Compensate by placing the decimal point in the product.
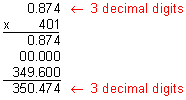
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 350.474 makes sense since it is close to our estimate of 400.
Answer: The product of 401 and 0.874 is 350.474.
Note that in Example 4, there are three decimal digits in the factor 0.874 and three decimal digits in the product. Since there is a zero in the tens place of the number 401, the second partial product consisted of zeros. Let's look at some more examples.
Example 5: Multiply: 40 x 3.5
Analysis: There is one decimal digit in the factor 3.5.
Step 1: Estimate the product.
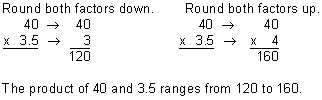
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
![]()
Compensate by placing the decimal point in the product.
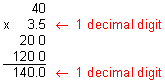
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 140.0 makes sense since the product of 40 and 3.5 ranges from 120 to 160.
Answer: The product of 40 and 3.5 is 140.0
Example 6: Multiply: 0.96 x 91
Analysis: There are two decimal digits in the factor 0.96.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
![]()
Compensate by placing the decimal point in the product.
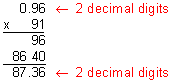
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 87.36 makes sense since it is close to our estimate of 90.
Answer: The product of 0.96 and 91 is 87.36.
Example 7: Multiply: 6,785 x 0.001
Analysis: There are three decimal digits in the factor 0.001.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
![]()
Compensate by placing the decimal point in the product.
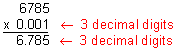
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 6.785 makes sense since it is close to our estimate of 7.
Answer: The product of 6,785 and .001 is 6.785.
Example 8: Look for a pattern. Then find each product using mental arithmetic.
| 35 x 698 | = | 24,430. |
| 3.5 x 698 | = | |
| 0.35 x 698 | = | |
| 35 x 0.698 | = |
Answer:
| 35 x 698 | = | 24,430. |
| 3.5 x 698 | = | 2,443. |
| 0.35 x 698 | = | 244.3 |
| 35 x 0.698 | = | 24.43 |
Example 9: What do each of these numbers have in common: 40, 0.001, 200?
Analysis:
| 40 | = | 4 x 10 |
| 0.001 | = | |
| 200 | = | 2 x 100 |
Answer: Each number can be written as the product of a single digit and a power of 10.
 Example 10: Gold costs $802.70 per ounce. How much would 4 ounces cost?
Example 10: Gold costs $802.70 per ounce. How much would 4 ounces cost?
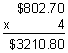
Answer: Four ounces of gold would cost $3,210.80.
Summary: When multiplying a decimal by a whole number, we use the following procedure:
- Estimate the product.
- Multiply to find the product.
- Multiply these numbers as if they were both whole numbers. Ignore the decimal point.
- Compensate by placing the decimal point in your product.
- Compare your estimate with your product to verify that your answer makes sense.
Estimating the product before we multiply lets us verify that the placement of the decimal point is correct, and that we have a reasonable answer. When we ignore a decimal point, we have really moved it to the right. Since we multiplied by a power of 10, we need to compensate to get the right answer. To do this, we must divide by that same power of 10 when we place the decimal point in our product: Start from the right of the last digit in the product, and move the decimal point the same number of places to the left.
Exercises
Directions: Read each question below. You may use paper and pencil to help you multiply. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. |
Multiply: 3.3 x 9 |
| 2. |
Multiply: 928 x 0.17 |
| 3. |
Multiply: $6.45 x 96 |
| 4. |
Multiply: 0.356 x 93 |
| 5. |
Danica Patrick can travel at 154.67 miles per hour in her race car. How far can she travel in 3 hours? |




