How To Divide Decimals
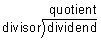 Problem 1: Do you see a pattern in each table below? Use mental arithmetic to find each quotient, then mouse over the red text.
Problem 1: Do you see a pattern in each table below? Use mental arithmetic to find each quotient, then mouse over the red text.
|
|||||||||||||||||||||
 Explanation: The patterns in the tables above were created by multiplying the divisor and the dividend by the same power of 10. In each pattern, the quotient remains the same. Thus, multiplying both the divisor and dividend by the same power of 10 maintains the equality of the expression.
Explanation: The patterns in the tables above were created by multiplying the divisor and the dividend by the same power of 10. In each pattern, the quotient remains the same. Thus, multiplying both the divisor and dividend by the same power of 10 maintains the equality of the expression.
Problem 2: Continue each pattern below by multiplying the divisor and the dividend by 10 until the divisor is a whole number. Then find each quotient.
|
|
|
Answer:
|
|
|
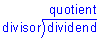 Let's compare Problems 1 and 2 above. In both problems, the quotients remain the same even though the divisors and dividends are multiplied by powers of 10. However, the divisors in Problem 1 are whole numbers; whereas the divisors in Problem 2 are decimals. Let's look at some examples of dividing by a decimal divisor.
Let's compare Problems 1 and 2 above. In both problems, the quotients remain the same even though the divisors and dividends are multiplied by powers of 10. However, the divisors in Problem 1 are whole numbers; whereas the divisors in Problem 2 are decimals. Let's look at some examples of dividing by a decimal divisor.
Example 1: ![]()
Analysis: The divisor is 0.8. To make it a whole number, we will multiply both the dividend and the divisor by 10.
| Multiply the divisor by a power of 10 to make it a whole number. | Multiply the dividend by the same power of 10. Place the decimal point in the quotient. | Divide the dividend by the whole-number divisor to find the quotient. | ||
Answer: The quotient of 9.6 and 0.8 is 12.
In Example 1, we changed the divisor to a whole number before performing the division. To do this, we multiplied both the divisor and the dividend by the same power of 10. Note that the quotient of 9.6 and 0.8 is the same as the quotient of 96 and 8. Let's look at why this is possible:
![]()
Thus, the quotient of 9.6 and 0.8 and the quotient of 96 and 8 are both 12. Let's look at another example.
Example 2: ![]()
Analysis: The divisor is 0.35. To make it a whole number, we will multiply both the dividend and the divisor by 100.
| Multiply the divisor by a power of 10 to make it a whole number. | Multiply the dividend by the same power of 10. Place the decimal point in the quotient. | Divide the dividend by the whole-number divisor to find the quotient. | ||
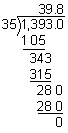 |
Answer: The quotient of 13.93 and 0.35 is 39.8
Note that in Example 1, the quotient is a whole number (12), and in Example 2, the quotient is a decimal (39.8).
Example 3: ![]()
Analysis: The divisor is 0.009. To make it a whole number, we will multiply both the dividend and the divisor by 1,000.
| Multiply the divisor by a power of 10 to make it a whole number. | Multiply the dividend by the same power of 10. Place the decimal point in the quotient. | Divide the dividend by the whole-number divisor to find the quotient. | ||
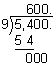 |
Answer: The quotient of 5.4 and 0.009 is 600.
Example 4:
![]()
Analysis: The divisor is 3.06. To make it a whole number, we will multiply both the dividend and the divisor by 100. After dividing, we will round the quotient to the nearest tenth.
| Multiply the divisor by a power of 10 to make it a whole number. | Multiply the dividend by the same power of 10. Place the decimal point in the quotient. | Divide the dividend by the whole-number divisor to find the quotient. | ||
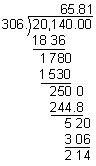 |
Answer: Rounded to the nearest tenth, the quotient of 201.4 and 3.06 is 65.8.
Example 5:
![]()
Analysis: The divisor is 5.3. To make it a whole number, we will multiply both the dividend and the divisor by 10. After dividing, we will round the quotient to the nearest cent (hundredth).
| Multiply the divisor by a power of 10 to make it a whole number. | Multiply the dividend by the same power of 10. Place the decimal point in the quotient. | Divide the dividend by the whole-number divisor to find the quotient. | ||
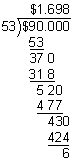 |
Answer: Rounded to the nearest cent, the quotient of $9 and 5.3 is $1.70.
 Example 6: A retailer has 802.7 units of goods to sell. If one shipping box only holds 0.875 units, then how many customers can she ship her goods to? Round your quotient to the nearest whole number.
Example 6: A retailer has 802.7 units of goods to sell. If one shipping box only holds 0.875 units, then how many customers can she ship her goods to? Round your quotient to the nearest whole number.
Analysis:
![]()
Divide:
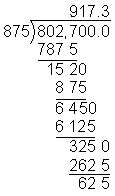
Answer: Rounded to the nearest whole number, the retailer can ship her goods to 917 customers.
Summary: When dividing by a decimal divisor, we use the following procedure:
- Multiply the divisor by a power of 10 to make it a whole number.
- Multiply the dividend by the same power of 10. Place the decimal point in the quotient.
- Divide the dividend by the whole-number divisor to find the quotient.
Exercises
Directions: Read each question below. You may use paper and pencil to help you divide. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. |
| 2. |
| 3. |
| 4. |
| 5. |
If 5.2 pounds of nails cost $16.96, then how much would 1 pound cost? Round your answer to the nearest cent. |




