Number Theory - Learn All About Integers; Numerals; Natural Numbers; Whole Numbers; Rational Numbers; Fractional Numbers and more!
Introduction
Those ten simple symbols, digits, or numbers that we all learn early in life that influence our lives in far more ways than we could ever imagine. Have you ever wondered what our lives would be like without these 10 elegant digits and the infinite array of other numbers that they can create? Birthdays, ages, height, weight, dimensions, addresses, telephone numbers, license plate numbers, credit card numbers, PIN numbers, bank account numbers, radio/TV station numbers, time, dates, years, directions, wake up times, sports scores, prices, accounting, sequences/series of numbers, magic squares, polygonal numbers, factors, squares, cubes, Fibonacci numbers, perfect, deficient, and abundant numbers, and the list goes on ad infinitum. Engineers, accountants, store clerks, manufacturers, cashiers, bankers, stock brokers, carpenters, mathematicians, scientists, and so on, could not survive without them. In a sense, it could easily be concluded that we would not be able to live without them. Surprisingly, there exists an almost immeasurable variety of hidden wonders surrounding or emanating from these familiar symbols that we use every day, the natural numbers.
Over time, many of the infinite arrays, or patterns, of numbers derivable from the basic ten digits have been categorized or classified into a variety of number types according to some purpose that they serve, fundamental rule that they follow, or property that they possess. Many, if not all, are marvelously unique and serve to illustrate the extreme natural beauty and wonder of our numbers as used in both classical and recreational mathematics.
In the interest of stimulating a broader interest in number theory and recreational mathematics, this collection will endeavor to present basic definitions and brief descriptions for several of the number types so often encountered in the broad field of recreational mathematics. The number type descriptions that follow will not be exhaustive in detail as space is limited and some would take volumes to cover in detail. A list of excellent reading references is provided for those who wish to learn more about any specific number type or explore others not included. It is sincerely hoped that the material contained herein will stimulate you to read and explore further. I also hope that after reading, digesting, and understanding the material offered herein, that you will have enjoyed the experience and that you will never utter those terrible, unforgettable words, "I hate math."
Some basic definitions of terms normally encountered in the classroom are given first.
Numbers - The Basics
Integers - Any of the positive and negative whole numbers, ..., -3, -2, -1, 0, +1, +2, +3, ... The positive integers, 1, 2, 3..., are called the natural numbers or counting numbers. The set of all integers is usually denoted by Z or Z+
Digits - the 10 symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, used to create numbers in the base 10 decimal number system.
Numerals - the symbols used to denote the natural numbers. The Arabic numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are those used in the Hindu-Arabic number system to define numbers.
Natural Numbers - the set of numbers, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,....., that we see and use every day. The natural numbers are often referred to as the counting numbers and the positive integers.
Whole Numbers - the natural numbers plus the zero.
Rational Numbers - any number that is either an integer "a" or is expressible as the ratio of two integers, a/b. The numerator, "a", may be any whole number, and the denominator, "b", may be any positive whole number greater than zero. If the denominator happens to be unity, b = 1, the ratio is an integer. If "b" is other than 1, a/b is a fraction.
Fractional Numbers - any number expressible by the quotient of two numbers as in a/b, "b" greater than 1, where "a" is called the numerator and "b" is called the denominator. If "a" is smaller than "b" it is a proper fraction. If "a" is greater than "b" it is an improper fraction which can be broken up into an integer and a proper fraction.
Irrational Numbers - any number that cannot be expressed by an integer or the ratio of two integers. Irrational numbers are expressible only as decimal fractions where the digits continue forever with no repeating pattern. Some examples of irrational numbers are 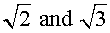
Transcendental Numbers - any number that cannot be the root of a polynomial equation with rational coefficients. They are a subset of irrational numbers examples of which are Pi = 3.14159... and e = 2.7182818..., the base of the natural logarithms.
Real Numbers - the set of real numbers including all the rational and irrational numbers.
Irrational numbers are numbers such as 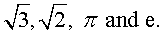
Rational numbers include the whole numbers (0, 1, 2, 3, ...), the integers (..., - 2, - 1, 0, 1, 2, ...), fractions, and repeating and terminating decimals.
Draw a line.
Put on it all the whole numbers 1,2,3,4,5,6,7.....etc
then put 0
then put all the negatives of the whole numbers to the left of 0
........-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0
Then put in all of the fractions .
Then put in all of the decimals [ some decimals aren't fractions ]
Now you have what is called the "real number line"
The way to get a number that is not "real" is to try to find the square root of - 1
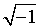 can't be 1 because 1 squared is 1, not -1
can't be 1 because 1 squared is 1, not -1
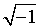 can't be -1 because the square of -1 is 1, not -1
can't be -1 because the square of -1 is 1, not -1
So there is no number on your number line to be 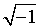
and new numbers would need to be put somewhere.
The number types currently entered, and/or planned to be entered, are listed below and will be updated as new entries are made in the future. When appropriate, and time permitting, some of the number definitions/descriptions will be expanded further to provide additional information.
Abundant, Algebraic, Amicable, Arrangement, Automorphic, Binary, Cardinal, Catalan, Complex, Composite, Congruent, Counting, Cubic, Decimal, Deficient, Even, Factor, Factorial, Fermat, Fibonacci, Figurate, Fractional, Friendly, Generating, Gnomon, Golden, Gyrating, Happy, Hardy-Ramanujan, Heronian, Imaginary, Infinite, Integers, Irrational, Mersenne, Monodigit, Narcissistic, Natural, Oblong, Octahedral, Odd, Ordinal, Parasite, Pell, Pentatope, Perfect , Persistent, Polygonal, Pronic, Pyramidal , Pythagorean, Quasiperfect, Random, Rational, Real, Rectangular, Relatively Prime, Semi-perfect, Sequence, Sociable, Square, Superabundant, Tag, Tetrahedral, Transcendental, Triangular, Unit Fraction, Whole.
Several of the numbers form unique patterns that are often used in the solution of mathematical problems. When distinct patterns are applicable, the first ten numbers of the patterns will be given along with specific relationships, or equations, that will enable you to find any number in the pattern.
--End of Introduction--
ABUNDANT NUMBERS
A number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n.
An abundant number is a number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n.
Abundant numbers are part of the family of numbers that are either deficient, perfect, or abundant.
Abundant numbers are numbers where the sum, Sa(N), of its aliquot parts/divisors is more than the number itself Sa(N) > N or S(N) > 2N. (In the language of the Greek mathematicians, the divisors of a number N were defined as any whole number smaller than N that, when divided into N, produced whole numbers. The factors/divisors of a number N, less the number itself, are referred to as the aliquot parts, aliquot divisors, or proper divisors, of the number.) Equivalently, N is also abundant if the sum, S(N), of "all" its divisors is greater than 2N.
From the following list
N-->.......1..2..3..4..5...6....7...8....9..10..11..12..13..14..15..16..17..18..19...20..21..22..23..24
Sa(N)-->1..1..1..3..1...6....1...7....4...8....1...16...1...10...9...15...1....21...1...22..11..12...1...36
S(N)--> 1..3..4..7..6..12...8..15..13.18..12..28..14..22..24..31..18...39..20..42..32..36..24..60
..........................................12,18,20, and 24 are abundant.
It can be readily seen that using the aliquot parts summation, sa(24) = 1+2+3+4+6+8+12 = 36 > N = 24 while s(24) = 1+2+3+4+6+8+12+24 = 60 > 2N = 48, making 24 abundant using either definition.
Only 21 of the numbers from 1 to 100 are abundant. The number 945 is the first odd abundant number.
Every even integer greater than 46 is expressible by the sum of two abundant numbers.
Every integer greater that 83,159 is expressible by the sum of two abundant numbers.
Any multiple of an abundant number is abundant.
A prime number or any power of a prime number is deficient. The divisors of a perfect or deficient number is deficient.
The abundant numbers below 100 are 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90 and 96.
(See perfect, semi-perfect, multiply-perfect, quasi-perfect, deficient, least deficient, super abundant)
ALGEBRAIC NUMBERS
Algebraic numbers are the real or complex number solutions to polynomial equations of the form:
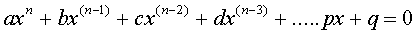
The coefficients a, b, c, d, ....p, q, are integers or fractions. All rational numbers are algebraic while some irrational numbers are algebraic.
ALIQUOT PART
An aliquot part is any divisor of a number, not equal to the number itself. The divisors are often referred to as proper divisors. The aliquot parts of the number 24 are 1, 2, 3,4, 6, 8 and 12..
ALMOST PERFECT NUMBER
An almost perfect number is typically applied to the powers of 2 since the sum of the aliquot parts is 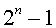
or just 1 short of being a perfect number. It follows that any power of 2 is a deficient number
ALPHAMETIC NUMBERS
Alphametic numbers form cryptarithms where a set of numbers are assigned to letters that usually spell out some meaningful thought. The numbers can form an addition, subtraction, multiplication or division problem. One of the first cryptarithms came into being in 1924 in the form of an addition problem the words being intended to represent a student's letter from college to the parents. The puzzle read SEND + MORE = MONEY. The answer was 9567 += 1085 = 10,652. Of course, you have to use logic to derive the numbers represented by each letter..
AMICABLE NUMBERS
Amicable numbers are pairs of numbers, each of which is the sum of the others aliquot divisors. For example, 220 and 284 are amicable numbers whereas all the aliquot divisors of 220, i.e., 110, 55, 44, 22, 10, 5, 4, 2, 1 add up to 284 and all the aliquot divisors of 284, i.e., 142, 71, 4, 2, 1 add up to 220. Also true for any two amicable numbers, N1 and N2, is the fact that the sum of all the factors/divisors of both, Sf(N1 + N2) = N1 + N2. Stated another way, Sf(220 + 284) = 220 + 284 = 504. Other amicable numbers are:
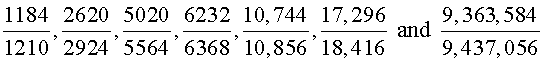
There are more than 1000 known amicable pairs. Amicable numbers are sometimes referred to as friendly numbers.
Several methods exist for deriving amicable numbers, though not all, unfortunately. An Arabian mathematician devised one method. For values of n greater than 1, amicable numbers take the form:
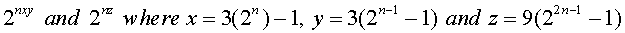
given that x, y, and z are prime numbers. n = 2 produces x = 11, y = 5 and z = 71 which are all prime and therefore result in the amicable number pair of 220/284. n = 3 produces the x = 23, y = 11 and z = 287 but 287 is composite, being 7x41. n = 4 produces x = 47, y = 23 and z = 1151, all prime, and thereby resulting in the amicable pair of 17,296 and 18,416. In reviewing the few amicable pairs shown earlier, it is obvious that this method does not produce all amicable pairs.
If the number 1 is not used in the addition of the aliquot divisors of two numbers, and the remaining aliquot divisors of each number still add up to the other number, the numbers are called semi-amicable. For example, the sum of the aliquot divisors of 48, excluding the 1, is 75 while the sum of the aliquot divisors of 75, excluding the 1, is 48.
As a matter of general information:
The sum of all the factors/divisors of a number N is given by
..................................Sf(N) = [p^(a+1) - 1] x [q^(b+1) - 1] x [r^(c+1) - 1]
.....................................................(p - 1).............(q - 1).............(r - 1)
which when applied to an example of 60 = 2^2x3x5 results in
..................................Sf(60) = (2^3 - 1) x (3^2 - 1) x (5^2 - 1) = 7 x 4 x 6 = 168.
......................................................1...............2..............4
Stated another way, the sum of the factors of a number N is given by
..................................Sf(N) = (1+p+p^2+....p^a)(1+q+q^2+....q^b)(1+r+r^2+....r^c)
which when applied to an example of 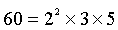
results in
.................................Sf(60) = (1+2+4)(1+3)(1+5) = 168.
As noted earlier, the sum of the aliquot factors/divisors is the sum of all the factors/divisors minus the number itself.
APOCALYPSE NUMBER
The apocalypse number, 666, often referred to as the beast number, is referred to in the bible, Revelations 13:18.
While the actual meaning or relevance of the number remain unclear, the number itself has some surprisingly interesting characteristics.
The sum of the first 36 positive numbers is 666 which makes it the 36th triangular number.
The sum of the squares of the first seven prime numbers is 666.
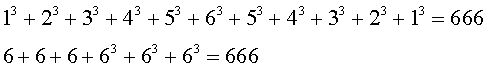
Multiplying the sides of the primitive right triangle 12-35-37 by 18 yields non-primitive sides of 216-630-666.
Even more surprising is the fact that these sides can be written in the Pythagorean Theorem form:
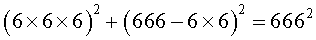
ARRANGEMENT NUMBERS
Arrangement numbers, more commonly called permutation numbers, or simply permutations, are the number of ways that a number of things can be ordered or arranged. They typically evolve from the question how many arrangements of "n" objects are possible using all "n" objects or "r" objects at a time. We designate the permutations of "n" things taken "n" at a time as nPn and the permutations of "n" things taken "r" at a time as nPr where P stands for permutations, "n" stands for the number of things involved, and "r" is less than "n". To find the number of permutations of "n" dissimilar things taken "n" at a time, the formula is nPn = n! which is "n" factorial which means:
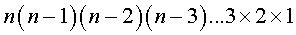
Example: How many ways can you arrange the letters A & B. Clearly 2 which is 2 x 1 = 2, namely AB and BA.
How many ways can you arrange the letters A, B & C in sets of three? Clearly 3P3 = 3 x 2 x 1 = 6, namely ABC, CBA, BAC, CAB, ACB, and BCA.
How many ways can you arrange A, B, C & D in sets of four? Clearly 4P4 = 4 x 3 x 2 x 1 = 24.
To find the number of permutations of "n" dissimilar things taken "r" at a time, the formula is:
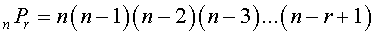
Example: How many ways can you arrange the letters A, B, C, and D using 2 at a time? We have 4P4 = 4 x (4-2+1) = 4 x 3 = 12 namely AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, and DC.
How many 3-place numbers can be formed from the digits 1, 2, 3, 4, 5, and 6, with no repeating digit? Then we have 6P3 = 6 x 5 x (6-3+1) = 6 x 5 x 4 = 120.
How many 3-letter arrangements can be made from the entire 26 letter alphabet with no repeating letters? We now have 26P3 = 26 x 25 x (26-3+1) = 26 x 25 x 24 = 15,600.
Lastly, four persons enter a car in which there are six seats. In how many ways can they seat themselves? 6P4 = 6 x 5 x 4 x (6-4+1) = 6 x 5 x 4 x 3 = 360.
Another permutation scenario is one where you wish to find the permutations of "n" things, taken all at a time, when "p" things are of one kind, "q" things of another kind, "r' things of a third kind, and the rest are all different. Without getting into the derivation,
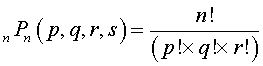
Example, how many different permutations are possible from the letters of the word committee taken all together? There are 9 letters of which 2 are m, 2 are t, 2 are e, and 1 c, 1 o, and 1 i. Therefore, the number of possible permutations of these 9 letters is:
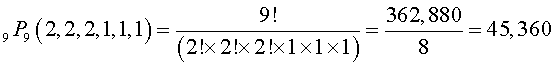
AUTOMORPHIC NUMBERS
Automorphic numbers are numbers of "n" digits whose squares end in the number itself. Such numbers must end in 1, 5, or 6 as these are the only numbers whose products produce 1, 5, or 6 in the units place. For instance, the square of 1 is 1; the square of 5 is 25; the square of 6 is 36.
What about 2 digit numbers ending in 1, 5, or 6? It is well known that all 2 digit numbers ending in 5 result in a number ending in 25 making 25 a 2 digit automorphic number with a square of 625. No other 2 digit numbers ending in 5 will produce an automorphic number.
Is there a 2 digit automorphic number ending in 1? We know that the product of 10A + 1 and 10A + 1 is 100A2 + 20A + 1. "A" must be a number such that 20A produces a number whose tens digit is equal to "A". For "A" = 2, 2 x 20 = 40 and 4 is not 2. For "A" = 3, 3 x 20 = 60 and 6 is not 3. Continuing in this fashion, we find no 2 digit automorphic number ending in 1.
Is there a 2 digit automorphic number ending in 6? Again, we know that the product of 10A + 6 and 10A + 6 is 100A2 + 120A + 36. "A" must be a number such that 120A produces a number whose tens digit added to 3 equals "A". For "A" = 2, 2 x 120 = 240 and 4 + 3 = 7 which is not 2. For "A" = 3, 3 x 120 = 360 and 6 + 3 = 9 which is not 3. Continuing in this manner through A = 9, for "A" = 7, we obtain 7 x 120 = 840 and 4 + 3 = 7 = "A" making 76 the only other 2 digit automorphic number whose square is 5776.
By the same process, it can be shown that the squares of every number ending in 625 or 376 will end in 625 or 376.
The sequence of squares ending in 25 are 25, 225, 625, 1225, 2025, 3025, etc. The nth square number ending in 25 can be derived directly from N(n)2 = 100n(n - 1) + 25. (This expression derives from the Finite Difference Series of the squares.)
BEAST NUMBER
See apocalypse number
BINARY NUMBERS
Binary numbers are the natural numbers written in base 2 rather than base 10. While the base 10 system uses 10 digits, the binary system uses only 2 digits, namely 0 and 1, to express the natural numbers in binary notation. The binary digits 0 and 1 are the only numbers used in computers and calculators to represent any base 10 number. This derives from the fact that the numbers of the familiar binary sequence, 1, 2, 4, 8, 16, 32, 64, 128, etc., can be combined to represent every number. To illustrate, 1 = 1, 2 = 2, 3 = 1 + 2, 4 = 4, 5 = 1 + 4, 6 = 2 + 4, 7 = 1 + 2 + 4, 8 = 8, 9 = 1 + 8, 10 = 2 + 8, 11 = 1 + 2 + 8, 12 = 4 + 8, and so on. In this manner, the counting numbers can be represented in a computer using only the binary digits of 0 and 1 as follows.
| Number | B I N A R Y S E Q U E N C E | |||||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||
| 1 | 1 | B | ||||||||
| 2 | 1 | 0 | I | |||||||
| 3 | 1 | 1 | N | |||||||
| 4 | 1 | 0 | 0 | A | ||||||
| 5 | 1 | 0 | 1 | R | ||||||
| 6 | 1 | 1 | 0 | Y | ||||||
| 7 | 1 | 1 | 1 | |||||||
| 8 | 1 | 0 | 0 | 0 | N | |||||
| 9 | 1 | 0 | 0 | 1 | O | |||||
| 10 | 1 | 0 | 1 | 0 | T | |||||
| 11 | 1 | 0 | 1 | 1 | A | |||||
| 12 | 1 | 1 | 0 | 0 | T | |||||
| 13 | 1 | 1 | 0 | 1 | I | |||||
| 14 | 1 | 1 | 1 | 0 | O | |||||
| 15 | 1 | 1 | 1 | 1 | N | |||||
| 76 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |||
| 157 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ||
As you can see, the location of the ones digit in the binary representation indicates the numbers of the binary sequence that are to be added together to yield the base 10 number of interest.
CARDINAL NUMBERS
A cardinal number is a number that defines how many items there are in a group or collection of items. Typically, an entire group of items is referred to as the "set" of items and the items within the set are referred to as the "elements" of the set. For example, the number, group, or set, of players on a baseball team is defined by the cardinal number 9. The set of 200 high school students in the graduating class is defined by the cardinal number 200. (See ordinal numbers and tag numbers.)
CATALAN NUMBERS
Catalan numbers are one of many special sequences of numbers that derive from combinatorics problems in recreational mathematics. Combinatorics deals with the selection of elements from a set of elements typically encountered under the topics of probability, combinations, permutations, and sampling. The specific Catalan numbers are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16,796 and so on deriving from
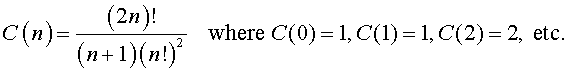
This particular set of numbers derive from several combinatoric problems, one of which is the following.
Given "2n" people gathered at a round table. How many person to person, non-crossing, handshakes can be made, i.e., no pairs of arms crossing one another across the table? A few quick sketches of circles with even sets of dots and lines will lead you to the first three answers easily. Two people, one handshake. Four people, two handshakes. Six people, 5 handshakes. With a little patience and perseverance, eight people will lead you to 14 handshakes. Beyond that, it is probably best to rely on the given expression.
CHOICE NUMBERS
Choice numbers, more commonly called combination numbers, or simply combinations, are the number of ways that a number of things can be selected, chosen, or grouped. Combinations concern only the grouping of items and not the arrangement of those items. They typically evolve from the question how many combinations of "n" objects are possible using all "n" objects or "r" objects at a time? To find the number of combinations of "n" dissimilar things taken "r" at a time, the formula is:
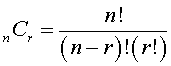
which can be stated as "n" factorial divided by the product of "r" factorial times (n - r) factorial.
Example: How many different ways can you combine the letters A, B, C, and D in sets of three? Clearly,
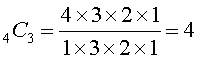
namely ABC, ABD, ACD, and BCD. (Note that ACB, BAC, BCA, CAB and CBA are all the same combination just arranged differently. In how many ways can a committee of three people be selected from a group of 12 people? We have:
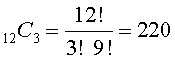
How many handshakes will take place between six people in a room when they each shakes hands with all the other people in the room one time? Here,
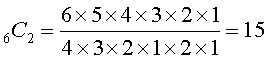
Notice that no consideration is given to the order or arrangement of the items but simply the combinations.
Another way of viewing combinations is as follows. Consider the number of combinations of 5 letters taken 3 at a time. This produces:
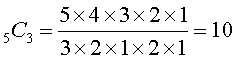
Now assume you permute (arrange) the r = 3 letters in each of the 10 combinations in all possible ways. Each group would produce r! permutations. Letting x = 5C3 for the moment, we would therefore have a total of x(r!) different permutations. This total, however, represents all the possible permutations (arrangements) of n things taken r at a time, which is shown under arrangement numbers and defined as nPr. Therefore,
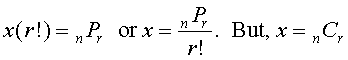
which results in
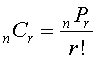
Using the committee of 3 out of 12 people example from above,
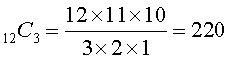
Consider the following: How many different ways can you enter a 4 door car? It is clear that there are 4 different ways of entering the car. Another way of expressing this is:
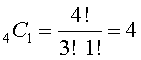
If we ignore the presence of the front seats for the purpose of this example, how many different ways can you exit the car assuming that you do not exit through the door you entered? Clearly you have 3 choices. This too can be expressed as:
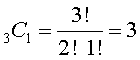
Carrying this one step further, how many different ways can you enter the car by one door and exit through another? Entering through door #1 leaves you with 3 other doors to exit through. The same result exists if you enter through either of the other 3 doors. Therefore, the total number of ways of entering and exiting under the specified conditions is:
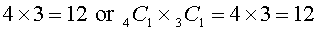
Another example of this type of situation is how many ways can a committee of 4 girls and 3 boys be selected from a class of 10 girls and 8 boys? This results in:
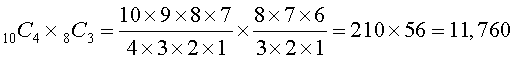
See ARRANGEMENT NUMBERS for determining the number of possible arrangements between items.
CIRCULAR PRIMES
A circular prime number is one that remains a prime number after repeatedly relocating the first digit of the number to the end of the number. For example, 197, 971 and 719 are all prime numbers. Similarly, 1193, 1931, 9311 and 3119 are all prime numbers. Other numbers that satisfy the definition are 11, 13, 37, 79, 113, 199 and 337.
Primes of two or more digits can only contain the digits 1, 3, 7 because, If 0, 2, 4, 5,6, or 8 were part of the number, in the units place, the number would be divisible by 2 or 5.
It is thought that there are an infinite number of circular primes but has not yet been proven.
COMPLEX NUMBERS
Complex numbers are formed by the addition of a real number and an imaginary number, the general form of which is a + bi where i = 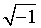
= the imaginary number and a and b are real numbers. The "a" is said to be the real part of the complex number and b the imaginary part.
COMPOSITE NUMBERS
Probably the easiest number to define after prime numbers.
The Fundamental Theorem of Arithmetic states that every positive integer greater than 1 is either a prime number or a composite number. As we know, a prime number "p" is any positive number the only divisors of which are 1 and p (or -1 and -p). Thus, by definition, any number that is not a prime number must be a composite number.
A composite number is any number having 3 or more factors/divisors and is the result of multiplying prime numbers together. Most of the positive integers are the product of smaller prime numbers.
Examples: 4, 6, 8, 10, 12, 14, 15, 16, 18, 20, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, etc., are all composite numbers, each being divisible by lower prime numbers. Every number divisible by 2, the only even prime, is composite.
Every composite number can be broken down to a single unique set of prime factors and their exponents.
Examples: 210 = 2 x 3 x 5 x 7; 495 = 32 x 51 x 111 or 4500 = 2 x 2 x 3 x 3 x 5 x 5 x 5 = 22 x 32 x 53. This is the one and only possible factorization of the number 210.
If a positive number N is evenly divisible by any prime number less than 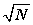
, the number N is composite.
Wilson's Theorem states that for every prime number "p", [(p + 1)! + 1] is evenly divisible by "p". The converse was shown to also be true in that every integer "N" that evenly divides [(N + 1)! + 1] is prime. Combining these leads to the famous general theorem that a necessary and sufficient condition that an integer "N" be prime is that "N" evenly divide [(n + 1)! + 1]. Conversely, if "N" does not divide [(N + 1)! + 1], "N" is composite.
Unfortunately, the practical use of this method is minimal due to the large numbers encountered with high N's.
CONGRUENT NUMBERS
A number N is said to be congruent if there are two integers, x and y, that result in the expressions x2 + Ny2 and x2 - Ny2 being perfect squares. The smallest known congruent number is 5 which satisfies 412 + 5(122) = 492 and 412 - 5(122) = 312. The use of the square of a negative number results in another solution of 22 + 5(12) = 32 and 22 - 5(12) = (-1)2. While there are many congruent numbers, finding them is an arduous task. The expressions x2 + Ny2 and x2 - Ny2 are often useful in solving many problems in recreational mathematics.
COUNTING NUMBERS
The counting numbers are the familiar set of whole numbers, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,....., that we see and use every day. (The 0 is sometimes included.) The set of counting numbers is often referred to as the natural numbers.
CUBIC NUMBERS or CUBES
A cubic number is the third power of a number as in a x a x a = a3. Those familiar with the evolution of the squares from adding successive odd numbers might not be too surprised to discover how the cubes evolve from summing odd numbers also. Clearly, the nth cube is simply n3. Cubes can be derived in other ways also:
The cube of any integer, "n", is the sum of the series of odd numbers beginning with (n2 - n + 1) and ending with (n2 + n - 1). Example: For n = 6, (n2 - n + 1) = 31 and 31 + 33 + 35 + 37 + 39 + 41 = 216 = 63.
| n3 | (n)3 | n3 | (n2 - n + 1) | (n2 + n - 1) | ||
| 1 | 13 | = | 1 | 1 | = | 1(1) |
| 2 | 23 | = | 8 | 3 + 5 | = | 2(1 + 2 + 1) |
| 3 | 33 | = | 27 | 7 + 9 + 11 | = | 3(1 + 2 + 3 + 2 + 1) |
| 4 | 43 | = | 64 | 13 + 15 + 17 + 19 | = | 4(1 + 2 + 3 + 4 + 3 + 2 + 1) |
| 5 | 53 | = | 125 | 21 + 23 + 25 + 27 + 29 | = | 5(1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1) |
Starting with
1....2....3....4....5....6....7....8....9....10....11....12....13....14....15....16....17....18....19....20....21
Cross out every third number giving us
1....2..........4....5.........7.....8..........10....11............13....14............16....17............19....20
Summing
1...3...........7...12.......19...27.........37....48............61....75...........91...108...........127..147
Cross out every second number giving us
1................7..............19................37....................61...................91....................127
Summing
1................8..............27................64..................125.................216....................343
The last line of numbers are the perfect cubes.
The first ten cubes are 1, 8, 27, 64, 125, 216, 343, 512, 729 and 1000.
The sum of the first n cubes starting with 1, is 13 + 23 + 33 +........+ n3.

which, quite surprisingly, is the square of the nth triangular number, defined by Tn = n(n+1)/2.
The sum of the cubes of the first n odd numbers is 2n4 - n2 = n2(2n2 - 1).
The sum of the cubes of the first n even numbers is 2n4 + 4n3 + 2n2 = 2n2(n + 1)2.
The sum of the first n cubes, 13 + 23 + 33 + 43 +........+ n3 is equal to the square of the sum of the first n integers. Thus, 13 + 23 + 33 + 43+........+ n3 = (1 + 2 + 3 + 4 +........+ n)2.
The cube of any integer is the difference of the squares of two other integers.
Every cube is either a multiple of 9 or right next to one.
A perfect cube can end in any of the digits 0 through 9.
Three digit numbers that are the sum of the cubes of their digits: 153, 370, 371, 407.
The smallest number that is the sum of 2 cubes in two different ways. 1729 = 13 + 123 = 103 + 93.
What are the dimensions of two cubes with integral sides that have their combined volume equal to the combined length of their edges. What are the dimensions of the cubes? x = 2 and y = 4.
The sum of any two cubes can never be a cube.
The sum of a series of three or more cubes can equal a cube.
Examples:
33 + 43 + 53 = 63
113 + 123 + 133 + 143 = 203
11343 + 11353 + .........21333 = 16,8303
The cube root of a number N is the number "a" which, when multiplied by itself twice, results in the number N or N = axaxa. There is no formula for extracting the cube root of a number. It can be obtained by means of a long division method or a simple estimation method.
The sum of "n" terms of an arithmetic progression with the first term equal to the sum of the first "n" natural numbers and a common difference of "n" is n3.
First, a method for approximating the cube root of a number to several decimal places which is usually sufficient for everyday use.
Estimation Method
1--Make an estimate of the cube root of N = n lying between successive integers a and b.
2--Compute A = N - a3 and B = b3 - N
2--n = a + (bA)/[bA + aB]
Example: Find the cube root of 146
1--With 146 lying between 125 and 216, let a = 5 and b = 6.
2--A = 21 and B = 70
3--n = 5 + (6 x 21)/[6 x 21 + 5 x 70] = 5 + 126/476 = 5 + .264 = 5.2647
4--The cube root of 146 is 5.2656
A more exact method for determining integer cube roots.
Note that each cube of the numbers 1 through 10 ends in a different digit:
n3....1......2......3......4......5......6.......7......8.......9......10
n3....1......8....27....64...125...216...343...512...729...1000
Also note that the last digit is the cube root for all cases except 2, 3, 7 and 8. A quick review of these exceptions leads to the fact that these four digits are the difference between 10 and the cube root, i.e., 8 = 10 - 2, 7 = 10 - 3, 3 = 10 - 7 and 2 = 10 - 8. How can this information be used to determine the cube root of a number?
Given the cube of a number between 1 and 100, say 300,763.
The last digit tells us that the last digit of the cube root is 10 - 3 = 7.
Eliminating the last 3 digits of the cube leaves the number 300.
The number 300 lies between the cubes of 6 and 7 in our listing above.
The first digit of our cube root will be the lowest of these two numbers, in this case 6.
Therefore, the cube root of 30,763 becomes 67.
Given the cube 592,704.
The last digit of 4 is the last digit of the cube root.
The number 592 lies between 512 and 729, the cubes of 8 and 9.
Therefore, the cube root of 592,704 becomes 84.
Of course, this is only useful if you know ahead of time that the cube is a perfect cube, i.e., having an integral cube root.
CYCLIC NUMBERS
A cyclic number is a number of "n" digits that when multiplied by 1, 2, 3,...n, results in the same digits but in a different order. For example, the number 142,857 is a cyclic number since 142,857 x 2 = 285,714, 142,857 x 3 = 428,571, 142,857 x 4 = 571,428, and so on. It is not known just how many cyclic numbers exist.
DECIMAL NUMBERS
Decimal numbers are numbers expressed through the decimal, or base 10, number system where each digit represents a multiple of some power of 10. The term applies primarily to numbers that have fractional parts so indicated by a decimal point. A number less than 1 is called a decimal fraction, e.g., .673. A mixed decimal is one consisting of an integer and a decimal fraction, e.g., 37.937.
Rational numbers can be expressed in the form of a fraction, 1/2, or as a decimal, .50, 1/8, or as a decimal, .125. From experience, we know that a fraction expressed in decimal form will either terminate without a remainder such as 3/8 = 0.375 or 7/8 = 0.875, repeat the same digit endlessly such as 1/3 = .3333333..... or 2/3 = .6666666....., repeat a series of different digits repeatedly such as 1/27 = .037037037... or 1/7 = .142857142857...., or repeat a series of digits after some non repeating digits such as 1/12 = .0833333.....
All prime denominators produce repeating decimals. Fractions with the same denominator often produce decimals with the same period and period length but with the digits starting with a different number in the period. For instance, 1/7 = .142857142857142857...., 2/7 = .285714285714285714...., 3/7 = .428571428571428571...., 4/7 = .571428571428571428...., 5/7 = .714285714285714285...., and 6/7 = .857142857142857142.... Other denominators produce two or more repeating periods in different orders. Investigate those with prime denominators of 11, 13, 17, 19, etc. and then 9, 12, 14, 16, 18, etc.and see what results. What do you notice?
Another interesting property of repeating decimals of even period length is illustrated by the following. Take the decimal equivalent of 2/7 = .285714285714...... The repeating period is 285714. Split the period into two groups of three digits and add them together. The result is 999. Do the same with any other repeating decimal period and the result will always be a series of nines. Take 1/17 = .0588235294117647........ Adding 05882352 and 94117647 gives you 99999999.
All repeating decimals, regardless of the period and length, are rational numbers. This simply means that it can be expressed as the quotient of two integers. A question that frequently arises is how to convert a repeating decimal, which we know to be rational, back to a fraction.
Rational decimal fractions may be converted to fractions as follows:
Given the decimal number N = 0.078078078...
Multiply N by 1000 or 1000N = 78.078078078...
Subtracting N = .078078078...
.................................999N = 78 making N = 78/999 = 26/333.
Given the decimal number N = .076923076923...
Muliply N by 1,000,000 or 1,000,000N = 76,923.0769230769230...
Subtracting N = .0769231769230...
.........................................999,999N = 76,923 making N = 76,923/999,999 = 1/13
An easier way to derive the fraction is to simply place the repeating digits over the same number of 9's. For example, the repeating decimal of .729729729729 converts to the fraction of 729/999 = 27/37.
Another trick where zeros are involved is to place the repeating digits over the same number of 9's with as many zeros following the 9's as there are zeros in the repeating decimal. For example, .00757575 leads to 075/9900 = 1/132.
DEFICIENT NUMBERS
Deficient numbers are part of the family of numbers that are either deficient, perfect, or abundant.
Deficient numbers, dN, are numbers where the sum of its aliquot parts (proper divisors), sa(N), is less than the number itself sa(N) < N. (In the language of the Greek mathematicians, the divisors of a number N were defined as any whole numbers smaller than N that, when divided into N, produced whole numbers. The factors/divisors of a number N, less the number itself, are referred to as the aliquot parts, or aliquot divisors, of the number.) Equivalently, N is also deficient if the sum, s(N), of all its divisors is less than 2N. It can be readily seen that using the aliquot parts summation, sa(16) = 1+2+4+8 = 14 < N = 16 while using all of the divisors, s(16) = 1+2+4+8+16 = 31 < 2N = 32, making the number 16 deficient under either definition.
From the following list
N-->.......1..2..3..4..5...6....7...8....9..10..11..12..13..14..15..16..17..18..19...20..21..22..23..24
Sa(N)-->1..1..1..3..1...6....1...7....4...8....1...16...1...10...9...15...1....21...1...22..11..12...1...36
S(N)--> 1..3..4..7..6..12...8..15..13.18..12..28..14..22..24..31..18...39..20..42..32..36..24..60
1,2,3,4,5,7,8,9,10,11,13,14,15,16,17,19,21,22,23 are all deficient.
A prime number or any power of a prime number is deficient. The divisors of a pefect or deficient number is deficient.
DIGITAL ROOT
The digital root of a number is the single digit that results from the continuous summation of the digits of the number and the numbers resulting from each summation. For example, consider the number 7935. The summation of its digits is 24. The summation of 2 and 4 is 6, the digital root of 7935. Digital roots are used to check addition and multiplication by means of a method called casting out nines. For example, check the summation of 378 and 942. The DR of 378 is 9, 3+7+8=18, 1+8=9.. The DR of 942 is 6, 9+4+2=15, 1+5=6. Adding 9 and 6 produces 15, The DR of 15 is 6, 1+5=6. The summation of 378 and 942 is 1320. The DR of 1320 is 6. With the two final DR's are equal, the addition is correct.
EGYPTIAN FRACTIONS
Egyptian fractions are the reciprocals of the positive integers where the numerator is always one. They are often referred to as unit fractions. They were used exclusively by the Egyptians to represent all forms of fractions. The two fractions that they used that did not have a unit fraction was 2/3 and 3/4. The only other fractions that they seemed to have a strong interest in were those of the form 2/n where n was any positive odd number. The Rhind papyrus contains a list of unit fractions representing a series of 2/n for odd n's from 5 to 501. It is unclear as to why they found these 2/n fractions so important. These and other 2/n fractions may be derived from 2/n = 1/[n(n+1)/2] + 1/[n+1)/2].
In the year 1202, Leonardo Fibonacci proved that any ordinary fraction could be expressed as the sum of a series of unit fractions in an infinite number of ways. He used the then named greedy method for deriving basic unit fraction expansions. He described the greedy method in his Liber Abaci as simply subtracting the largest unit fraction less than the given non unit fraction and repeating the process until only unit fractions remained. It was later shown that the greedy method, when applied to any fraction m/n, results in a series of no more than "m" unit fractions. An example will best illustrate the process.
Reduce the fraction 13/17 to a sum of unit fractions. Dividing the fraction yields .7647. Of the unit fractions 1/2, 1/3, 1/4, 1/5, etc., 1/2 is the largest that is smaller than 13/17 so we compute 13/17 - 1/2 = 9/34 making 13/17 = 1/2 + 9/34. Repeating with 9/34, we have 9/34 - 1/4 = 2/136 = 1/68 making 13/17 = 1/2 + 1/4 + 1/68. Alternatively, divide the numerator into the denominator and use the next highest integer as the new denominator. 17/13 = 1.307 making 2 the denominator of the fraction to be subtracted from 13/17.
Reduce the fraction 23/37 to a sum of unit fractions. 23/37 - 1/2 = 9/74 - 1/16 = 70/1184 - 1/17 = 6/20,128 - 1/3355 = 1/33,764,720 making 23/37 = 1/2 + 1/16 + 1/17 + 1/3355 + 1/33,764,720.
There are many methods or algorithms that derive the unit fractions for any fraction m/n. Much more information regarding unit fractions can be found at
Unit Fractions Search at http://mathpages.com/cgi-local/AT-mathpakbsearch.cgi
Egyptian Fractions at http://www1.ics.uci.edu/~eppstein/numth/egypt/
Unit Fraction from Math World at http://mathworld.wolfram.com/UnitFraction.html
Algorithms for Egyptian Fractions at http://www1.ics.uci.edu/~eppstein/numth/egypt/force.html
Creating Unit Fractions at http://www.mathpages.com/home/kmath150.html
The unit fractions derived by means of the method shown, or any other method, can be further broken down into other unit fractions by means of the identity 1/a = 1/(a+1) + 1/a(a+1), also known to Fibonacci. For example, 1/2 = 1/(2+1) + 1/2(2+1) = 1/3 + 1/6. Further still, 1/3 = 1/(3+1) + 1/3(3+1) = 1/4 + 1/12 and 1/6 = 1/(6+1) + 1/6(6+1) = 1/7 + 1/42 yielding 1/2 = 1/4 + 1/7 + 1/12 + 1/42. While the number of unit fractions derivable for any given fraction is therefore infinite, there is apparently no known procedure for deriving a series with the least number of unit fractions or the smallest largest denominator. .
EQUABLE TRIANGLES
A shape is called equable if its area equals its perimeter. There are exactly five equable Heronian triangles: the ones with side lengths (5,12,13), (6,8,10), (6,25,29), (7,15,20), and (9,10,17).
EQUIVALENT NUMBERS
Equivalent numbers are numbers where the aliquot parts (proper divisors other than the number itself) are identical. For instance, 159, 559 and 703 are equivalent numbers since their aliquot parts sum to 57.
f(159) = 1, 3, 53 and 159 where 1 + 3 + 53 = 57.
f(559) = 1, 13, 43 and 559 where 1 + 13 + 43 = 57.
f(703) = 1, 19, 37 and 703 where 1 + 19 + 37 = 57.
EVEN NUMBERS
Probably the easiest number to define, an even number is any number that is evenly divisible by 2.
The nth even number is given by Ne = 2n.
The sum of the set of "n" consecutive even numbers beginning with 2 is given by Se = n(n + 1).
The sum of the set of m consecutive even numbers starting with n1 and ending with n2 is given by Se(n1-n2) = n2^2 - n1^2 + (n1 + n2) or (n1 + n2)(1 + n1 - n2).
The sum of the squares of the even numbers starting with 2^2 is given by Se^2 = (4n^3 + 6n^2 + 2n)/3.
An even number multiplied by any number, or raised to any power, results in another even number.
The number 2 is the only even prime number.




